题目内容
9.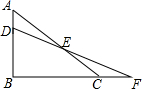 已知:如图,在△ABC中,点D在边AB上,且AD=$\frac{1}{3}$AB.点F在边BC的延长线上,连结DF,交AC于点E,设$\frac{CF}{BF}$=k.求:$\frac{CE}{AE}$的值.
已知:如图,在△ABC中,点D在边AB上,且AD=$\frac{1}{3}$AB.点F在边BC的延长线上,连结DF,交AC于点E,设$\frac{CF}{BF}$=k.求:$\frac{CE}{AE}$的值.
分析 作CG∥AB交DF于G,如图,先由CG∥AB得到$\frac{CG}{AB}$=$\frac{CF}{BF}$=k,则CG=kAB,再由CG∥AD得到$\frac{CG}{AD}$=$\frac{CE}{AE}$,然后利用比例性质可得到$\frac{CE}{AE}$=3k.
解答 解:作CG∥AB交DF于G,如图,
∵CG∥AB,
∴$\frac{CG}{AB}$=$\frac{CF}{BF}$=k,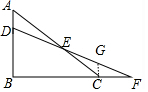
∴CG=kAB,
∵CG∥AD,
∴$\frac{CG}{AD}$=$\frac{CE}{AE}$,
而CG=kAB,AD=$\frac{1}{3}$AB,
∴$\frac{CE}{AE}$=$\frac{kAB}{\frac{1}{3}AB}$=3k.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.熟练掌握比例的性质.

练习册系列答案
相关题目
17.已知AB=6cm,C是AB的中点,那么AC为多长( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
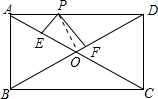 如图,在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,PE⊥BD,PE⊥AC,E、F分别是垂足,求PE+PF的长.
如图,在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,PE⊥BD,PE⊥AC,E、F分别是垂足,求PE+PF的长. 如图所示,∠B=∠D,∠A=∠C,求证:∠1=∠2.
如图所示,∠B=∠D,∠A=∠C,求证:∠1=∠2.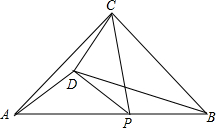 如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD.
如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD. 如图,已知AB∥CD,DF交AC于点E,交AB于点F,若E是AC的中点.求证:点E是DF的中点.
如图,已知AB∥CD,DF交AC于点E,交AB于点F,若E是AC的中点.求证:点E是DF的中点. 如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹)
如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹)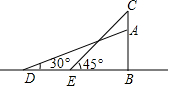 如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)
如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)