题目内容
11.解方程(1)$\frac{3}{x-2}$-$\frac{x}{2-x}$=-2
(2)$\frac{x}{2x-5}$-$\frac{5}{5-2x}$=1
(3)$\frac{3}{x+1}$+$\frac{2x}{x+1}$=2
(4)$\frac{{a}^{2}-4a}{{a}^{2}-1}$+1=$\frac{2a}{a+1}$.
分析 (1)方程两边同乘(x-2)化分式方程为整式方程求解即可;
(2)方程两边同乘(2x-5)化分式方程为整式方程求解即可;
(3)方程两边同乘(x+1)化分式方程为整式方程求解即可;
(4)方程两边同乘(a+1)(a-1)化分式方程为整式方程求解即可.
解答 解:(1)方程两边同乘(x-2)得:
3+x=-2,
解得x=-5.
经检验x=-5是原方程的解.
故原方程的解为:x=-5.
(2)方程两边同乘(2x-5)得:
x+5=2x-5,
解得x=10.
经检验x=10是原方程的解.
故原方程的解为:x=10.
(3)方程两边同乘(x+1)得:
3+2x=2(x+1),
3=2,
故原方程无解.
(4)方程两边同乘(a+1)(a-1)得:
a2-4a+a2-1=2a(a-1),
解得a=-$\frac{1}{2}$.
经检验a=-$\frac{1}{2}$是原方程的解.
故原方程的解为:a=-$\frac{1}{2}$.
点评 本题考查解分式方程的能力,(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
16.方程4(a-x)-4(x+1)=60的解是x=1,则a的值为( )
| A. | -14 | B. | 20 | C. | 18 | D. | -16 |
 如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹)
如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹)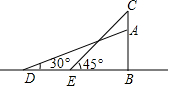 如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)
如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号) 如图,粮仓的顶部是圆锥形,此圆锥底面的直径为12m,母线长为8m,为防雨需在粮仓的顶部铺上油毡,若铺油毡的费用为30元/m2,则共需花4520元.(π取3.14,精确到10元)
如图,粮仓的顶部是圆锥形,此圆锥底面的直径为12m,母线长为8m,为防雨需在粮仓的顶部铺上油毡,若铺油毡的费用为30元/m2,则共需花4520元.(π取3.14,精确到10元)