题目内容
10.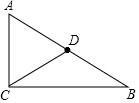 如图,在Rt△ABC中,∠C=90°,AC=9cm,BC=12cm,点D是AB的中点,现在以C点为圆心画圆,使A,B,D三点满足一点在⊙C外,一点在⊙C上,一点在⊙C内,求⊙C的半径.
如图,在Rt△ABC中,∠C=90°,AC=9cm,BC=12cm,点D是AB的中点,现在以C点为圆心画圆,使A,B,D三点满足一点在⊙C外,一点在⊙C上,一点在⊙C内,求⊙C的半径.
分析 根据勾股定理求出AB,求出CD,根据点和圆的位置关系得出即可.
解答 解:由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{9}^{2}+1{2}^{2}}$=15,
∵点D为直角三角形ABC斜边上的中点,
∴CD=$\frac{1}{2}$AB=7.5,
∵以C点为圆心画圆,使A,B,D三点满足一点在⊙C外,一点在⊙C上,一点在⊙C内,CA=9cm,CB=12cm,CD=7.5cm,
∴⊙O的半径为9cm.
点评 本题考查了勾股定理,点和圆的位置关系,直角三角形斜边上的中线性质的应用,能理解点和圆的位置关系内容是解此题的关键.

练习册系列答案
相关题目
 如图所示,∠B=∠D,∠A=∠C,求证:∠1=∠2.
如图所示,∠B=∠D,∠A=∠C,求证:∠1=∠2. 如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹)
如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹)
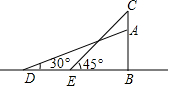 如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)
如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)