题目内容
5.某市决定对欲引进种植的A、B两种绿色蔬果实行政府补贴.据分析得到以下两条信息:信息一:对于A种蔬果,所获收益yA(万元)与补贴金额x(万元)之间满足正比例函数关系:yA=kx;
信息二:对于B种蔬果,所获收益yB(万元)与补贴金额x(万元)之间满足二次函数关系:yB=ax2+bx;
| x/万元 | 1 | 2 |
| yA/万元 | 0.6 | 1.2 |
| yB/万元 | 2.4 | 4.4 |
填空:yA=0.6xyB=-0.2x2+2.6x.
分析 将x=1、yA=0.6代入yA=kx求出k的值可得yA解析式,将x=1、yB=2.4,x=2、yB=4.4代入yB=ax2+bx列方程组求出a、b的值可得yB的解析式.
解答 解:根据题意,将x=1、yA=0.6代入yA=kx,得:k=0.6,
∴yA=0.6x;
将x=1、yB=2.4,x=2、yB=4.4代入yB=ax2+bx,
得:$\left\{\begin{array}{l}{a+b=2.4}\\{4a+2b=4.4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-0.2}\\{b=2.6}\end{array}\right.$,
∴yB=-0.2x2+2.6x;
故答案为:0.6x,-0.2x2+2.6x.
点评 此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
20.若方程x2-3x-4=0的两根分别为x1和x2,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值是( )
| A. | 1 | B. | 2 | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
10.一个多边形的每个内角均为120°,则这个多边形是( )
| A. | 七边形 | B. | 六边形 | C. | 五边形 | D. | 四边形 |
14.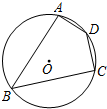 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )| A. | π | B. | 2π | C. | 4π | D. | 8π |
 如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为4:9.
如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为4:9.