题目内容
13．
如图，△ABC与△DEF是位似图形，位似比为2：3，则△ABC与△DEF的面积比为4：9．
分析 由△ABC与△DEF是关于点O的位似图形，且位似比为2：3，又由相似三角形的面积比等于相似比的平方，即可求得△ABC与△DEF的面积比．
解答 解：∵△ABC与△DEF是关于点O的位似图形，△ABC与△DEF的位似比为：2：3，
∴△ABC与△DEF的相似比为：2：3，
∴△ABC与△DEF的面积比为：4：9．
故答案为：4：9．
点评 本题考查了位似的相关知识，位似是相似的特殊形式，位似比等于相似比，其对应的面积比等于相似比的平方．
练习册系列答案
相关题目
3．函数y=x+3与y=$-\frac{2}{x}$的图象的交点为（a，b），则$\frac{1}{a}-\frac{1}{b}$的值是（ ）
| A． | $-\frac{3}{2}$ | B． | $\frac{3}{2}$ | C． | $-\frac{2}{3}$ | D． | $\frac{2}{3}$ |
如图，⊙O的半径是2，∠ACB=30°，则小扇形AOB的面积是$\frac{2}{3}$π（结果保留π）．
8．
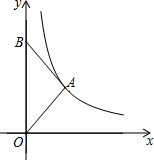如图，在平面直角坐标系中，点B在y轴上，第一象限内点A满足AB=AO，反比例函数y=$\frac{k}{x}$的图象经过点A，若△ABO的面积为2，则k的值为（ ）
如图，在平面直角坐标系中，点B在y轴上，第一象限内点A满足AB=AO，反比例函数y=$\frac{k}{x}$的图象经过点A，若△ABO的面积为2，则k的值为（ ）| A． | 1 | B． | 2 | C． | 4 | D． | $\frac{1}{2}$ |
18．
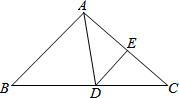如图，△ABC周长为36cm，把其边AC对折，使点C、A重合，折痕交BC边于点D，交AC边于点E，连结AD，若AE=6cm，则△ABD的周长是（ ）
如图，△ABC周长为36cm，把其边AC对折，使点C、A重合，折痕交BC边于点D，交AC边于点E，连结AD，若AE=6cm，则△ABD的周长是（ ）| A． | 24cm | B． | 26cm | C． | 28cm | D． | 30cm |
5．某市决定对欲引进种植的A、B两种绿色蔬果实行政府补贴．据分析得到以下两条信息：
信息一：对于A种蔬果，所获收益yA（万元）与补贴金额x（万元）之间满足正比例函数关系：yA=kx；
信息二：对于B种蔬果，所获收益yB（万元）与补贴金额x（万元）之间满足二次函数关系：yB=ax2+bx；
其中，yA、yB（万元）与补贴金额x（万元）的部分对应值如上表所示：
填空：yA=0.6xyB=-0.2x2+2.6x．
信息一：对于A种蔬果，所获收益yA（万元）与补贴金额x（万元）之间满足正比例函数关系：yA=kx；
信息二：对于B种蔬果，所获收益yB（万元）与补贴金额x（万元）之间满足二次函数关系：yB=ax2+bx；
| x/万元 | 1 | 2 |
| yA/万元 | 0.6 | 1.2 |
| yB/万元 | 2.4 | 4.4 |
填空：yA=0.6xyB=-0.2x2+2.6x．
2．
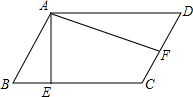如图，已知?ABCD中，AE⊥BC，AF⊥DC，BC：CD=3：2，AB=EC，则∠EAF=（ ）
如图，已知?ABCD中，AE⊥BC，AF⊥DC，BC：CD=3：2，AB=EC，则∠EAF=（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 80° |