题目内容
9. 一辆货车和一辆轿车先后从甲地出发向终点乙地行驶.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.根据图象,有下列说法:
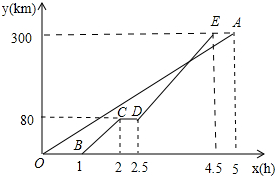
一辆货车和一辆轿车先后从甲地出发向终点乙地行驶.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.根据图象,有下列说法:①甲乙两地相距300千米;
②货车是匀速行驶,速度为60千米/小时;
③轿车中途休息了0.5小时,休息后的速度为$\frac{200}{3}$千米/小时;
④轿车从甲地出发后经过2.9小时追上货车;
以上说法中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据函数的图象即可直接求解;②根据函数的图象即可直接求解;③根据函数的图象即可得出轿车中途休息时间,再利用路程、时间和速度的关系得出轿车的速度;④求得直线OA和DE的解析式,求得交点坐标,即可求得轿车追上货车的时间.
解答 解:由图象可知:甲乙两地相距300千米,故①正确;
由图象可知:货车是匀速行驶,速度=300÷5=60千米/小时,故②正确;
由图象可知:轿车中途休息了2.5-2=0.5小时,休息后的速度为(300-80)÷(4.5-2.5)=110千米/小时,故③错误;
设线段DE的解析式是y=kx+b,
根据题意得:$\left\{\begin{array}{l}{2.5k+b=80\\;}\\{4.5k+b=300}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=110}\\{b=-195}\end{array}\right.$,
则一次函数的解析式是:y=110x-195,
设OA的解析式是:y=mx,
根据题意得:5m=300,
解得:m=60,
则函数解析式是:y=60x,
根据题意得:$\left\{\begin{array}{l}{y=110x-195\\;}\\{y=60x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3.9}\\{y=234}\end{array}\right.$.
则轿车从甲地出发后经过3.9-1=2.9小时追上货车,故④正确;
故选C
点评 此题为一次函数的应用,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义.

练习册系列答案
相关题目
19.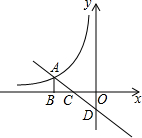 如图,平面直角坐标系中,直线y=kx-1与反比例函数$y=-\frac{6}{x}$相交于点A,AB⊥x轴,S△ABC=1,则k的值为( )
如图,平面直角坐标系中,直线y=kx-1与反比例函数$y=-\frac{6}{x}$相交于点A,AB⊥x轴,S△ABC=1,则k的值为( )
 如图,平面直角坐标系中,直线y=kx-1与反比例函数$y=-\frac{6}{x}$相交于点A,AB⊥x轴,S△ABC=1,则k的值为( )
如图,平面直角坐标系中,直线y=kx-1与反比例函数$y=-\frac{6}{x}$相交于点A,AB⊥x轴,S△ABC=1,则k的值为( )| A. | $-\frac{1}{8}$ | B. | $\frac{1}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{1}{2}$ |
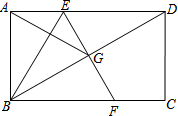 已知在矩形ABCD中,点E为边AD上一点,点A关于BE的对称点G位于对角线BD上,EG的延长线交边BC于点F.
已知在矩形ABCD中,点E为边AD上一点,点A关于BE的对称点G位于对角线BD上,EG的延长线交边BC于点F.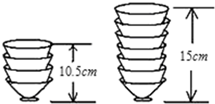 如图,两摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给的数据信息,解答下列问题:
如图,两摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给的数据信息,解答下列问题: 下面设想用电脑模拟台球游戏,为简单起见,约定:
下面设想用电脑模拟台球游戏,为简单起见,约定: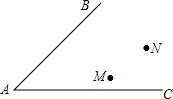 如图,两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个饮水供应点P,使P到两条道路的距离相等,且使PM=PN.有一同学说:“只要作一个角平分线、一条线段的垂直平分线,这个茶水供应点的位置就确定了”,你认为这位同学说得对吗?请说明理由,并通过作图找出这一点,不写作法,保留作图痕迹.
如图,两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个饮水供应点P,使P到两条道路的距离相等,且使PM=PN.有一同学说:“只要作一个角平分线、一条线段的垂直平分线,这个茶水供应点的位置就确定了”,你认为这位同学说得对吗?请说明理由,并通过作图找出这一点,不写作法,保留作图痕迹.