题目内容
14. 下面设想用电脑模拟台球游戏,为简单起见,约定:
下面设想用电脑模拟台球游戏,为简单起见,约定:(1)每个球或球袋都视为一点,如不遇障碍,各球均沿直线前进;
(2)A球击中B球,意味着B球在A球前进的路线上,且B球被撞击后沿着A球原来的方向前进;
(3)球撞及桌边后的反弹角等于入射角.
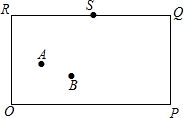
如图,在矩形台球桌OPQR上,OP=200cm,OR=120cm桌面上只剩下白球A和6号球B,白球A到台球桌OR边的距离为40cm,到台球桌边OP的距离为60cm,6号球B到台球桌OR边的距离为70cm,到台球桌边OP的距离为30cm,希望A球撞击桌边OP上C点后反弹,再击中B球.
(1)利用直尺和圆规作出点C的位置,并求OC的长度.(不写作法,保留作图痕迹)
(2)桌边RQ中点有球袋S,通过计算判定6号球B被从C点反弹出的白球撞击后,能否落入球袋S中(假定6号球B被撞击后的速度足够大).
分析 (1)作A点关于x轴的对称点A',连接A'B,则A'B与x轴的交点即为电脑所要找的点C,利用待定系数法求出直线A'B的解析式,进而得出C点的坐标;
(2)根据S(100,120)的坐标满足直线y=3x-180解析式,即可得出6号球被从C点反弹出的白球撞击后,能够直接落入球袋S中.
解答  解:(1)如图,作A点关于x轴的对称点A',连接A'B,则A'B与x轴的交点即为电脑所要找的点C,
解:(1)如图,作A点关于x轴的对称点A',连接A'B,则A'B与x轴的交点即为电脑所要找的点C,
由A(40,60)得A'(40,-60),设直线A'B的解析式为y=kx+b,
则由$\left\{\begin{array}{l}{-60=40k+b}\\{30=70k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=3}\\{b=-180}\end{array}\right.$,
∴直线CB的解析式:y=3x-180;
将y=0代入,得出x=60,
∴求出直线AB'与x轴的交点坐标,C点的坐标为(60,0),故OC=60;
(2)因为S(100,120)的坐标满足直线y=3x-180解析式,
所以6号球被从C点反弹出的白球撞击后,能够直接落入球袋S中.
点评 此题主要考查了一次函数的综合应用,根据已知得出直线CB的解析式进而利用在图象上点的坐标性质得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知圆的面积为7π,估计该圆的半径r所在范围正确的是( )
| A. | 1<r<2 | B. | 2<r<3 | C. | 3<r<4 | D. | 4<r<5 |
5.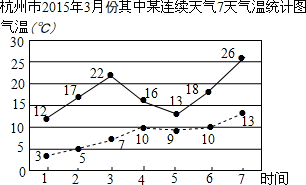 如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):
如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):
①这7天中温差最大的达13℃;
②这7天中各天最高气温与最低气温成正比关系;
③最高气温的中位数是17;
④该7天杭城气温变化较大.
你认为正确的是( )
 如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):
如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):①这7天中温差最大的达13℃;
②这7天中各天最高气温与最低气温成正比关系;
③最高气温的中位数是17;
④该7天杭城气温变化较大.
你认为正确的是( )
| A. | ①②③④ | B. | ①② | C. | ①③ | D. | ③④ |
4.虽然近几年无锡市政府加大了太湖水治污力度,但由于大规模、高强度的经济活动和日益增加的污染负荷,使部分太湖水域水质恶化,富营养化不断加剧.为了保护水资源,我市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
| 月用水量(吨) | 单价(元/吨) |
| 不大于10吨部分 | 1.5 |
| 大于10吨不大于m吨部分(20≤m≤50) | 2 |
| 大于m吨部分 | 3 |
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
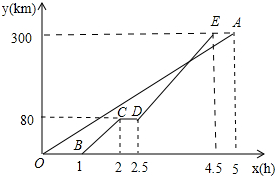 一辆货车和一辆轿车先后从甲地出发向终点乙地行驶.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.根据图象,有下列说法:
一辆货车和一辆轿车先后从甲地出发向终点乙地行驶.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.根据图象,有下列说法: 如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2.
如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2.