题目内容
17.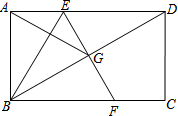 已知在矩形ABCD中,点E为边AD上一点,点A关于BE的对称点G位于对角线BD上,EG的延长线交边BC于点F.
已知在矩形ABCD中,点E为边AD上一点,点A关于BE的对称点G位于对角线BD上,EG的延长线交边BC于点F.(1)求证:AE≠ED;
(2)求证:△BEF是等腰三角形;
(3)若△BEF是正三角形,且AB=1,求EF的长.
分析 (1)由轴对称的性质得出AE=EG,在Rt△EGD中,ED>EG,ED>AE,即可得出结论;
(2)由(1)知∠AEB=∠BEG,再由 AD∥BC,得出∠AEB=∠EBF,证出∠BEG=∠EBF,即可得出结论;
(3)由△BEF是正三角形,得出∠AEB=60°,证出BG=GD,由BD=2,设EF=2x,则 BG=$\sqrt{3}$x.得出 2$\sqrt{3}$x=2,得出2x=$\frac{2\sqrt{3}}{3}$,即可得出EF.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵点A与点G关于BE对称,
∴BE垂直平分AG,∠BAD=∠BGE=90°,
∴AE=EG.
在Rt△EGD中,ED>EG,
∴ED>AE,
即AE≠ED;
(2)证明:由(1)知∠AEB=∠BEG,
又∵AD∥BC,
∴∠AEB=∠EBF,
∴∠BEG=∠EBF,
∴△BEF是等腰三角形;
(3)解:∵△BEF是正三角形,
则∠AEB=60°,BD=2AB=2,
∵∠ABE=∠EBG=30°,
∴∠DBC=30°,
∴BG⊥EF,EG=GF,
∴BG=GD,
又∵BD=2,
设EF=2x,则 BG=$\sqrt{3}$x.
∴2$\sqrt{3}$x=2,
∴2x=$\frac{2\sqrt{3}}{3}$,
即EF=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了矩形的性质、等腰三角形的判定与性质、等边三角形的性质、轴对称的性质;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
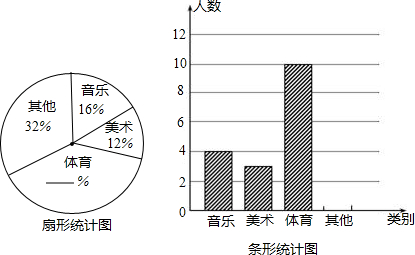
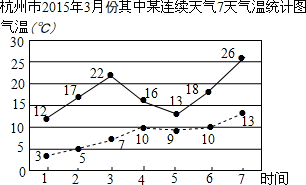 如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):
如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):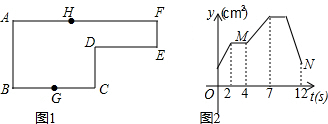
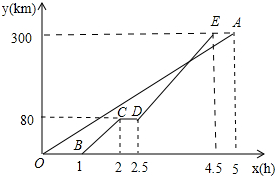 一辆货车和一辆轿车先后从甲地出发向终点乙地行驶.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.根据图象,有下列说法:
一辆货车和一辆轿车先后从甲地出发向终点乙地行驶.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.根据图象,有下列说法: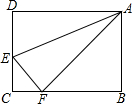 如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2.
如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2.