题目内容
2.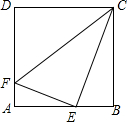 已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状.
已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状.
分析 因为正方形ABCD的边长为4,易得AF=1,则FD=3,DC=BC=4,AE=EB=2;在Rt△AEF、Rt△DFC,Rt△EBC中,利用勾股定理求出EF、EC、FC的长,再根据勾股定理的逆定理解答.
解答 解:△EFC为直角三角形.
∵正方形ABCD的边长为4,
∴AF=1,FD=3,DC=BC=4,AE=EB=2;
在Rt△AEF中,EF=$\sqrt{{AF}^{2}{+AE}^{2}}$=$\sqrt{5}$;
在Rt△DFC中,FC=$\sqrt{{FD}^{2}{+CD}^{2}}$=5;
在Rt△EBC中,EC=$\sqrt{{EB}^{2}{+BC}^{2}}$=2$\sqrt{5}$.
∴EC2+EF2=FC2,
∴△EFC是直角三角形.
点评 本题考查了勾股定理和勾股定理的逆定理及正方形的性质,利用勾股定理求出三角形三边长,再利用勾股定理逆定理解答是解答此题的关键.

练习册系列答案
相关题目
13.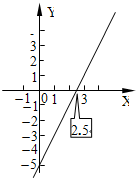 如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是
如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是
( )
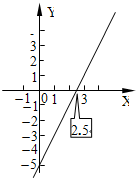 如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是
如图,已知一次函数y=kx+b,观察图象回答问题:当kx+b>0,x的取值范围是( )
| A. | x>2.5 | B. | x<2.5 | C. | x>-5 | D. | x<-5 |
10.下列运算正确的是( )
| A. | x3x2=x6 | B. | (-2x3)(-3x2)=6x5 | C. | (-2x)2=-4x2 | D. | x2+x2=2x4 |
14.下列运算正确的是( )
| A. | a3+a3=a6 | B. | a2•a2=a4 | C. | (2a)4=2a4 | D. | a6÷a3=a2 |
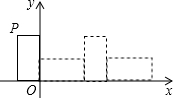 如图,把小矩形放在第二象限,使两条边与坐标轴重合,然后将小矩形无滑动的沿x轴顺时针滚动,每一次边落在x轴上记作一次操作,己知顶点P(-1,2),则经过2015次操作后点P的坐标为(3021,0).
如图,把小矩形放在第二象限,使两条边与坐标轴重合,然后将小矩形无滑动的沿x轴顺时针滚动,每一次边落在x轴上记作一次操作,己知顶点P(-1,2),则经过2015次操作后点P的坐标为(3021,0).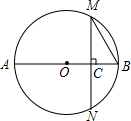 如图,AB是圆O的直径,C是AB的一个四等分点,过C作AB的垂线交圆O于M,N两点,连结MB,则cos∠MBA=$\frac{1}{2}$.
如图,AB是圆O的直径,C是AB的一个四等分点,过C作AB的垂线交圆O于M,N两点,连结MB,则cos∠MBA=$\frac{1}{2}$.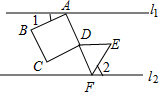 如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )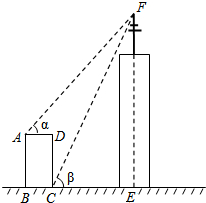 如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.
如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.