题目内容
17.已知一次函数y=(3a+2)x-(4-b),问实数a,b取何值时,使得:(1)y随x的增大而减小?
(2)图象经过第二、三、四象限?
(3)图象与y轴的交点在x轴上方?
(4)图象经过原点?
分析 (1)由函数为减函数,可知k=3a+2<0,解不等式即可得出结论;
(2)由函数图象经过第二、三、四象限,可知k<0,b>0,套入数据,解不等式组即可得出结论;
(3)由图象与y轴的交点在x轴上方,可知b=-(4-b)>0,解不等式即可得出结论;
(4)函数图形若过原点,则b=-(4-b)=0,解方程即可得出结论.
解答 解:(1)由已知得:3a+2<0,
解得:a<-$\frac{2}{3}$.
故当a<-$\frac{2}{3}$时,y随x的增大而减小.
(2)由已知得:$\left\{\begin{array}{l}{3a+2<0}\\{4-b>0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a<-\frac{2}{3}}\\{b<4}\end{array}\right.$.
故当a<-$\frac{2}{3}$且b<4时,图象经过第二、三、四象限.
(3)由已知得:4-b<0,
解得:b>4.
故当b>4时,图象与y轴的交点在x轴上方.
(4)由已知得:4-b=0,
解得:b=4.
故当b=4时,图象经过原点.
点评 本题考查了一次函数图象与系数的关系,解题的关键是根据已知找出不等式(或不等式组).本题属于基础题,难度不大,解决该题型题目时,根据给定函数图象的情况,结合一次函数图象与系数的关系得出关于一次函数系数的不等式(或不等式组)是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
7.下列说法错误的是( )
| A. | 27的立方根是3 | B. | (-1)2010是最小的正整数 | ||
| C. | 两个无理数的和一定是无理数 | D. | 实数与数轴上的点一一对应 |
5.计算(2a3)3的结果是( )
| A. | 6a6 | B. | 8a6 | C. | 6a9 | D. | 8a9 |
6.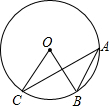 如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
 如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{2}$ |
7.下列运算正确的是( )
| A. | a•a2=a2 | B. | a+2a=3a | C. | (2a)2=2a2 | D. | (x+2)(x-3)=x2-6 |
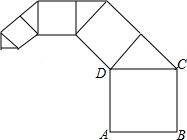 如图,正方形ABCD的边长是2,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2…按此规律继续下去,则S2016的值为($\frac{1}{2}$)2013.
如图,正方形ABCD的边长是2,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2…按此规律继续下去,则S2016的值为($\frac{1}{2}$)2013. 如图,E是正方形ABCD的边BC的延长线上的一点,连接AE交DC于点F 若BC=4,CE=5,求CF的长.
如图,E是正方形ABCD的边BC的延长线上的一点,连接AE交DC于点F 若BC=4,CE=5,求CF的长.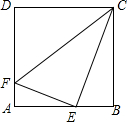 已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状.
已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状.