题目内容
7.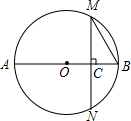 如图,AB是圆O的直径,C是AB的一个四等分点,过C作AB的垂线交圆O于M,N两点,连结MB,则cos∠MBA=$\frac{1}{2}$.
如图,AB是圆O的直径,C是AB的一个四等分点,过C作AB的垂线交圆O于M,N两点,连结MB,则cos∠MBA=$\frac{1}{2}$.
分析 首先连接OM,由已知易得∠BOM=60°,继而可得△OBM是等边三角形,继而求得答案.
解答  解:连接OM,
解:连接OM,
∵AB是圆O的直径,C是AB的一个四等分点,
∴OC=$\frac{1}{2}$OM,
∵MN⊥AB,
∴cos∠BOM=$\frac{OC}{OM}$=$\frac{1}{2}$,
∴∠BOM=60°,
∵OB=OM,
∴△OBM是等边三角形,
∴∠MBA=60°,
∴cos∠MBA=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查了圆周角定理、等边三角形的判定与性质以及特殊角的三角函数问题.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
15.下列运算中正确的是( )
| A. | $\sqrt{16}$=±4 | B. | 100${\;}^{-\frac{1}{2}}$=-10 | C. | $\root{4}{(-3)^{4}}$=-3 | D. | |$\sqrt{8}$-3|=3-$\sqrt{8}$ |
19.下列运算正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | B. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ | C. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{(2-\sqrt{5})^{2}}$=2-$\sqrt{5}$ |
16.已知等腰三角形两边长分别为3和5,第三边是方程x2-5x+6=0的解,则这个三角形的周长是( )
| A. | 9 | B. | 10 | C. | 11 | D. | 14 |
 [实际情境]
[实际情境] 如图,在正方形ABCD中,AB=$\sqrt{2}$,点P为边AB上一动点(不与A、B重合),过A、P在正方形内部作正方形APEF,交边AD于F点,连接DE、EC,当△CDE为等腰三角形时,AP=$\sqrt{2}$-1或$\frac{\sqrt{2}}{2}$.
如图,在正方形ABCD中,AB=$\sqrt{2}$,点P为边AB上一动点(不与A、B重合),过A、P在正方形内部作正方形APEF,交边AD于F点,连接DE、EC,当△CDE为等腰三角形时,AP=$\sqrt{2}$-1或$\frac{\sqrt{2}}{2}$.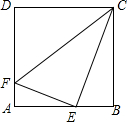 已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状.
已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状.