题目内容
11.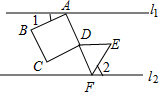 如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )| A. | 30° | B. | 60° | C. | 45° | D. | 15° |
分析 根据平行线的性质可以先求出∠3=∠4=60°,再根据∠1=180°-∠BAD-∠3进行计算即可.
解答 解: 如图,∵四边形ABCD是正方形,
如图,∵四边形ABCD是正方形,
∴∠BAD=90°,
∵△DEF是等边三角形,
∴∠DFE=60°,
∵l1∥l2,
∴∠3=∠4,
∵∠2=60°,∠DFE=60°,
∴∠3=∠4=180°-∠DFE-∠2=60°.
∵∠BAD=90°,
∴∠1=180°-∠BAD-∠3=30°,
故选A.
点评 本题考查正方形、等边三角形的性质、平行线的性质.熟练掌握这些性质是解决问题的关键,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列运算正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | B. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ | C. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{(2-\sqrt{5})^{2}}$=2-$\sqrt{5}$ |
6.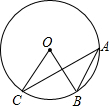 如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
 如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )
如图,⊙O经过A,B,C三点,∠BOC=60°,则sinA等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{2}$ |
16.已知等腰三角形两边长分别为3和5,第三边是方程x2-5x+6=0的解,则这个三角形的周长是( )
| A. | 9 | B. | 10 | C. | 11 | D. | 14 |
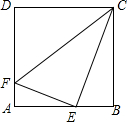 已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状.
已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=$\frac{1}{4}$AD,试判断△EFC的形状.


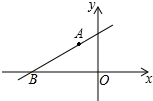 如图,直线y=kx+b经过A(-1,2)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-2x的解集为-$\sqrt{7}$<x<-1.
如图,直线y=kx+b经过A(-1,2)和B(-$\sqrt{7}$,0)两点,则不等式0<kx+b<-2x的解集为-$\sqrt{7}$<x<-1.