题目内容
4．根据下列问题列方程，并将所列方程化成一元二次方程的一般形式：（1）一个圆的面积是2πm2，求半径；
（2）一个直角三角形的两条直角边相差3cm，面积是9cm2，求较长的直角边的长．
分析 （1）直接利用圆的面积公式进而得出答案；
（2）直接利用直角三角形面积求法得出答案．
解答 解：（1）设圆的半径为：x，
∵一个圆的面积是2πm2，
∴2π=πx2，
解得：x=$\sqrt{2}$，
答：半径为$\sqrt{2}$m；
（2）设较长的直角边的长为xcm，则较短边长为：（x-3）cm，根据题意可得：
$\frac{1}{2}$（x-3）x=9，
整理得：x2-3x-18=0，
解得：x1=-3，x2=6，
答：较长的直角边的长为6cm．
点评 此题主要考查了由实际问题抽象出一元二次方程，正确得出等式是解题关键．
练习册系列答案
相关题目
14．我市为实现“四城同创”目标，绿化办计划为某新开发住宅小区购买并种植400株树苗，某苗圃公司提供以下信息：
①可供选择的树苗有杨树、柳树和樟树三种，并且要求购买杨树、柳树的数量相等．
②如表：
设购买杨树、樟树的数量分别为x株、y株．
（1）写出y与x之间的函数关系式（不要求写出自变量的取值范围）；
（2）当每株樟树的批发价p等于3元时，要使这400棵树苗两年后对该住宅小区的空气净化指数不低于90，就怎样安排这三种树苗的购买数量，才能使购买树苗的总费用最低？最低总费用是多少？
（3）当每株樟树批发价p（元）与购买数量y（株）之间存在关系p=3-0.005y时，求购买树苗的总费用W（元）与购买杨树数量x（株）之间的函数关系式（不要求写出自变量的取值范围）．
①可供选择的树苗有杨树、柳树和樟树三种，并且要求购买杨树、柳树的数量相等．
②如表：
| 树苗 | 每株树批发价格（元） | 两年后每株树苗对空气的净化指数 |
| 杨树 | 3 | 0.4 |
| 柳树 | 2 | 0.1 |
| 樟树 | p | 0.2 |
（1）写出y与x之间的函数关系式（不要求写出自变量的取值范围）；
（2）当每株樟树的批发价p等于3元时，要使这400棵树苗两年后对该住宅小区的空气净化指数不低于90，就怎样安排这三种树苗的购买数量，才能使购买树苗的总费用最低？最低总费用是多少？
（3）当每株樟树批发价p（元）与购买数量y（株）之间存在关系p=3-0.005y时，求购买树苗的总费用W（元）与购买杨树数量x（株）之间的函数关系式（不要求写出自变量的取值范围）．
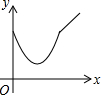
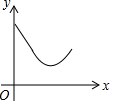
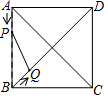如图，正方形ABCD中，动点P的运动路线为AB→BC，动点Q的运动路线为对角线BD，点P，Q以同样的速度分别从A，B两点同时出发匀速前进，当一个点到达终点停止运动时，另一个点也随之停止．设点P的运动路程为x，PQ的长为y，则下列能大致表示y与x的函数关系的图象为（ ）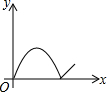
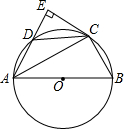已知：如图，四边形ABCD内接于⊙O，AB是⊙O的直径，CE切⊙O于C，AE⊥CE，交⊙O于D．
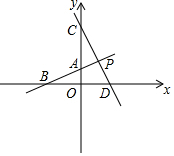如图，直线AB与坐标轴分别交于点A、点B，且OA、OB的长分别为方程x2-6x+8=0的两个根（OA＜OB），点C在y轴上，且OA：AC=2：5，直线CD垂直于直线AB于点P，交x轴于点D．