题目内容
19.观察下列等式:$\frac{1}{1×3}$=$\frac{1}{2}$(1-$\frac{1}{3}$),$\frac{1}{3×5}$=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$),$\frac{1}{5×7}$=$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$),…(1)猜想并写出第n个等式;
【猜想】
(2)计算:$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2015×2017}$.
分析 (1)根据所给出的等式找出规律,即可得出第n个算式;
(2)根据(1)得出的规律解答即可.
解答 解:(1)第n个等式为:$\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$;
(2)$\frac{1}{1×3}+\frac{1}{3×5}+\frac{1}{5×7}+…\frac{1}{2015×2017}$
=$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+\frac{1}{2015}-\frac{1}{2017})$
=$\frac{1}{2}(1-\frac{1}{2017})$
=$\frac{1008}{2017}$.
点评 此题考查数字的变化规律,发现规律,利用规律解决问题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
9. 如图,△ABC中,AB=AC,D在BC上,∠BAD=50°,AE=AD,则∠EDC的度数为( )
如图,△ABC中,AB=AC,D在BC上,∠BAD=50°,AE=AD,则∠EDC的度数为( )
 如图,△ABC中,AB=AC,D在BC上,∠BAD=50°,AE=AD,则∠EDC的度数为( )
如图,△ABC中,AB=AC,D在BC上,∠BAD=50°,AE=AD,则∠EDC的度数为( )| A. | 15o | B. | 25o | C. | 30o | D. | 50o |
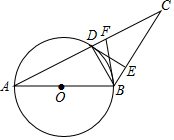 如图,在⊙O中,直径AB=8,∠A=30°,AC=8$\sqrt{3}$,AC与⊙O交于点D.
如图,在⊙O中,直径AB=8,∠A=30°,AC=8$\sqrt{3}$,AC与⊙O交于点D.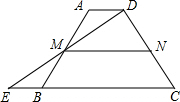 如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.
如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.