题目内容
2.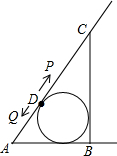 如图,△ABC中,CB=8,AB=6,AC=10,△ABC的内切圆交 AC于点D,点P从D出发,沿射线DC每次前进一个单位,点Q从D出发沿DA和射线AB每次前进a个单位,a为正整数且1≤a<5,当t次前进后△APQ与△ABC相似,所有满足条件的t为8、16、32.
如图,△ABC中,CB=8,AB=6,AC=10,△ABC的内切圆交 AC于点D,点P从D出发,沿射线DC每次前进一个单位,点Q从D出发沿DA和射线AB每次前进a个单位,a为正整数且1≤a<5,当t次前进后△APQ与△ABC相似,所有满足条件的t为8、16、32.
分析 首先在Rt△ABC中,根据AB=6,AC=10,BC=8,求出OD、AD的值各是多少;然后求出当t次前进后,点P前进的距离是t,点Q前进的距离是at,再分两种情况:(1)当∠APQ=90°时;(2)当∠AQP=90°时;根据a为正整数且1≤a<5,求出所有满足条件的t的值即可.
解答 解:如图,连接OD、OE、OF,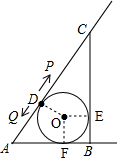 ,
,
∵Rt△ABC中AB=6,AC=10,BC=8,
∴(AB+BC+AC)×OD÷2=AB×BC÷2,
∴OD=6×8÷(6+8+10)=48÷24=2,
设AD=x,
则CD=CE=10-x,
BE=BF=8-(10-x)=x-2,
AF=AD=6-(x-2)=8-x,
∴x=8-x,
解得x=4,
∴当t次前进后,点P前进的距离是t,点Q前进的距离是at,
(1)当∠APQ=90°时,
∵△APQ与△ABC相似,
∴$\frac{AP}{AB}$=$\frac{AQ}{AC}$,
∴$\frac{AP}{AQ}$=$\frac{AB}{AC}$=$\frac{6}{10}$=$\frac{3}{5}$,
∴$\frac{t+4}{at-4}$=$\frac{3}{5}$,
整理,可得t=$\frac{32}{3a-5}$,
∵a为正整数且1≤a<5,
∴a=2时,t=32;a=3时,t=8.
(2)当∠AQP=90°时,
∵△APQ与△ABC相似,
∴$\frac{AQ}{AP}$=$\frac{AB}{AC}$,
∴$\frac{at-4}{t+4}$=$\frac{3}{5}$,
整理,可得t=$\frac{32}{5a-3}$,
∵a为正整数且1≤a<5,
∴a=1时,t=16.
综上,可得所有满足条件的t为8、16、32.
故答案为:8、16、32.
点评 本题主要考查三角形的内切圆与内心、相似三角形的判定与性质,掌握三角形的内心到三角形三边的距离相等和依据相似三角形的判定讨论分类是解题的关键.

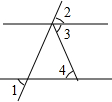 如图,已知∠1=∠2,∠3=65°,则∠4=( )
如图,已知∠1=∠2,∠3=65°,则∠4=( )| A. | 115° | B. | 55° | C. | 25° | D. | 65° |
| A. | $\sqrt{2}×3\sqrt{2}=4\sqrt{2}$ | B. | $\sqrt{24}$$÷\sqrt{6}$=2 | C. | $\sqrt{12}$$+\sqrt{18}$=6$\sqrt{3}$ | D. | $\sqrt{20}$-$\sqrt{5}$=4 |
 已知a,b表示有理数,在数轴上用点表示如图所示,且|a|>1>|b|,请完成下列各题:
已知a,b表示有理数,在数轴上用点表示如图所示,且|a|>1>|b|,请完成下列各题: 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°,现给出以下四个结论:
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°,现给出以下四个结论: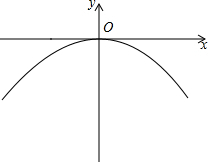 有一座抛物线形拱桥,正常水位时,桥下水面宽20m,拱顶距离水面4m.
有一座抛物线形拱桥,正常水位时,桥下水面宽20m,拱顶距离水面4m.