题目内容
5.如图,抛物线y=ax2+bx+2交x轴于A(-1,0),B(4,0)两点,交y轴于点C,过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.(1)求抛物线解析式;
(2)求点D坐标;
(2)连AC,将直线AC以每秒1个单位的速度向x轴的正方向运动,设运动时间为t秒,直线AC扫过梯形OCDB的面积为S,直接写出S与t的函数关系式;
(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q′.是否存在点P,使Q′恰好落在x轴上?若存在,求出此时点P的坐标;若不存在,说明理由.
分析 (1)将点A(-1,0)、B(4,0)代入y=ax2+bx+2中,解方程组即可.
(2)根据点D与点C的纵坐标相同,即可解决问题.
(3)分三种情形①当0≤t≤1时,如图1中,重叠部分是△CEC′,②当1<t≤3时,如图2中,重叠部分是梯形OCC′A′,③当3<t≤5时,如图3中,重叠部分是五边形OCDEA′.分别求解即可.
(4)存在.设直线PQ交x轴于F,点P坐标(a,-$\frac{1}{2}$a2+$\frac{3}{2}$a+2),分两种情形①当P在y轴右侧时,如图4中,由△COQ′∽△Q′FP,得$\frac{Q′C}{CO}$=$\frac{Q′P}{FQ′}$,求出FQ′,OQ′,
②当P在y轴左侧时,如图5中,由△COQ′∽△Q′FP,得$\frac{Q′C}{CO}$=$\frac{Q′P}{FQ′}$,求出FQ′,OQ′,即可解决问题.
解答 解:(1)将点A(-1,0)、B(4,0)代入y=ax2+bx+2中,
$\left\{\begin{array}{l}{0=a-b+2}\\{0=16a+4b+2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
(2)当x=0时,y=2,
∴C(0,2).
当y=2时,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=2,解得:x1=0,x2=3,
∴点D的坐标为(3,2).
(3)①当0≤t≤1时,如图1中,重叠部分是△CEC′,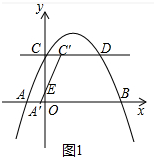
s=$\frac{1}{2}$•CC′•EC=$\frac{1}{2}$•t•2t=t2.
②当1<t≤3时,如图2中,重叠部分是梯形OCC′A′,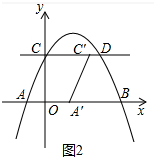
S=$\frac{t+(t-1)}{2}•$2=2t-2.
③当3<t≤5时,如图3中,重叠部分是五边形OCDEA′,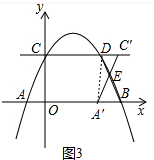
∵DC′∥A′B,
∴$\frac{DC′}{A′B}$=$\frac{ED}{EB}$=$\frac{t-3}{5-t}$,
∴$\frac{EB}{DB}$=$\frac{5-t}{2}$,
∴S△A′EB=$\frac{5-t}{2}$•S△A′DB=$\frac{5-t}{2}$•(5-t),
∴S=S梯形COBD-S△EA′B=-$\frac{1}{2}$t2+5t-$\frac{11}{2}$.
(4)存在满足条件的点P,显然点P在直线CD下方,设直线PQ交x轴于F,点P坐标(a,-$\frac{1}{2}$a2+$\frac{3}{2}$a+2),
①当P在y轴右侧时,如图4中,CQ=a,PQ=2-(-$\frac{1}{2}$a2+$\frac{3}{2}$a+2)=$\frac{1}{2}$a2-$\frac{3}{2}$a,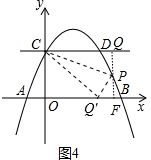
∵∠CQ′O+∠FQ′P=90°,∠COQ′=∠Q′FP=90°,∴∠FQ′P=∠OCQ′,
∴△COQ′∽△Q′FP,
∴$\frac{Q′C}{CO}$=$\frac{Q′P}{FQ′}$,
∴$\frac{a}{2}$=$\frac{\frac{1}{2}{a}^{2}-\frac{3}{2}a}{Q′F}$,
∴Q′F═a-3,
∴OQ′=OF-Q′F=a-(a-3)=3,CQ=CQ′=$\sqrt{C{O}^{2}+O{Q}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
此时a=$\sqrt{13}$,
∴点P坐标($\sqrt{13}$,$\frac{-9+3\sqrt{13}}{2}$),
②当P在y轴左侧时,如图5中,此时a<0,-$\frac{1}{2}$a2+$\frac{3}{2}$a+2<0,CQ=-a,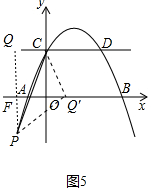
PQ=2-(-$\frac{1}{2}$a2+$\frac{3}{2}$a+2)=$\frac{1}{2}$a2-$\frac{3}{2}$a,
∵∠CQ′O+∠FQ′P=90°,∠CQ′O+∠OCQ′=90°,
∴∠FQ′P=∠OCQ′,∵∠COQ′=∠Q′FP=90°,
∴△COQ′∽△Q′FP,
∴$\frac{Q′C}{CO}$=$\frac{Q′P}{FQ′}$,
∴$\frac{-a}{2}$=$\frac{\frac{1}{2}{a}^{2}-\frac{3}{2}a}{FQ′}$,
∴FQ′=3-a,
∴OQ′=3,CQ=CQ′=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
此时a=-$\sqrt{13}$,点P坐标(-$\sqrt{13}$,$\frac{-9-\sqrt{13}}{2}$),
综上所述,点P坐标为($\sqrt{13}$,$\frac{-9+3\sqrt{13}}{2}$)或(-$\sqrt{13}$,$\frac{-9-\sqrt{13}}{2}$).
点评 本题考查二次函数综合题、平移变换、翻折变换、相似三角形的判定和性质、勾股定理等知识,解题的关键是熟练应用这些知识解决问题,学会分类讨论,学会正确寻找相似三角形,利用相似三角形的性质解决问题,体现了转化和数形结合的思想,属于中考压轴题.

 如图所示,在A处观察C,得仰角∠CAD=31°,且A、B的水平距离AE=800米,AB的坡度i=1:2,索道BC的坡度i=2:3,CD⊥AD于D,BF⊥CD于F.则索道BC的长大约是( )(参考数据:tan31°≈0.6,cos31°≈0.9,$\sqrt{13}$≈3.6)
如图所示,在A处观察C,得仰角∠CAD=31°,且A、B的水平距离AE=800米,AB的坡度i=1:2,索道BC的坡度i=2:3,CD⊥AD于D,BF⊥CD于F.则索道BC的长大约是( )(参考数据:tan31°≈0.6,cos31°≈0.9,$\sqrt{13}$≈3.6)| A. | 1400 | B. | 1440 | C. | 1500 | D. | 1540 |
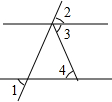 如图,已知∠1=∠2,∠3=65°,则∠4=( )
如图,已知∠1=∠2,∠3=65°,则∠4=( )| A. | 115° | B. | 55° | C. | 25° | D. | 65° |
 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°,现给出以下四个结论:
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°,现给出以下四个结论: