题目内容
17.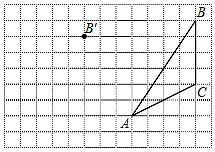 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC平移后得到△A′B′C′,图中点B′为点B的对应点.
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC平移后得到△A′B′C′,图中点B′为点B的对应点.(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出△ABC中AB边上的中线CD;
(3)画出△ABC中BC边上的高线AE;
(4)△A′B′C′的面积为8.
分析 (1)直接利用得出平移后对应点位置进而得出答案;
(2)直接利用中线的定义得出答案;
(3)直接利用高线的作法得出答案;
(4)直接利用三角形面积求法得出答案.
解答  解:(1)如图所示:△A′B′C′,即为所求;
解:(1)如图所示:△A′B′C′,即为所求;
(2)如图所示:CD即为所求;
(3)如图所示:AE即为所求;
(4))△A′B′C′的面积为:$\frac{1}{2}$×4×4=8.
故答案为:8.
点评 此题主要考查了平移变换以及三角形面积求法和三角形中线、高线的作法,正确把握相关定义是解题关键.

练习册系列答案
相关题目
7.在平面直角坐标系中,将抛物线y=x2-4先向右平移2个单位,再向上平移2个单位,得到的抛物线的表达式是( )
| A. | y=(x-2)2-2 | B. | y=(x+2)2+2 | C. | y=(x-2)2+2 | D. | y=(x+2)2-2 |
8.若一次函数y=ax+b的图象经过第一、二、四象限,则下列不等式中总是成立的是( )
| A. | ab>0 | B. | a-b>0 | C. | a+b>0 | D. | a2+b>0 |
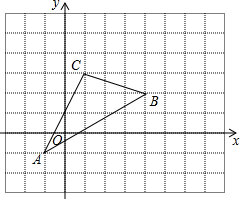 如图,在平面直角坐标系中,△ABC的顶点C的坐标为(1,3).
如图,在平面直角坐标系中,△ABC的顶点C的坐标为(1,3).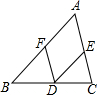 如图,点D在BC上,DE∥AB,交AC于点E,F是AB上的一个点.
如图,点D在BC上,DE∥AB,交AC于点E,F是AB上的一个点.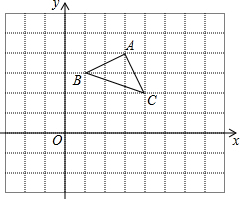 在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(-1,1),现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点,请画出平移后的△A′B′C′,并直接写出点B′、C′的坐标:B′(-3,0)、C′(0,-1).
在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(-1,1),现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点,请画出平移后的△A′B′C′,并直接写出点B′、C′的坐标:B′(-3,0)、C′(0,-1).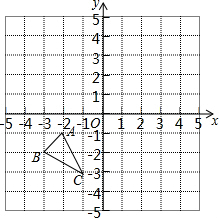 如图,在方格纸中,以O为旋转中心,将格点△ABC按顺时针方向旋转
如图,在方格纸中,以O为旋转中心,将格点△ABC按顺时针方向旋转