题目内容
2.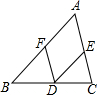 如图,点D在BC上,DE∥AB,交AC于点E,F是AB上的一个点.
如图,点D在BC上,DE∥AB,交AC于点E,F是AB上的一个点.(1)若DF平分∠BDE,∠B=50°,求∠DFB的度数;
(2)当∠A=∠FDE时,试说明DF∥AC的理由.
分析 (1)求出∠BDF=∠FDE,根据平行线的性质得出∠BFD=∠FDE,求出∠BFD=∠BDF,即可求出答案;
(2)根据平行线的性质得出∠FDE=∠BFD,求出∠A=∠BFD,根据平行线的判定得出即可.
解答 解:(1)∵DF平分∠BDE,
∴∠BDF=∠FDE,
∵DE∥AB,
∴∠BFD=∠FDE,
∴∠BFD=∠BDF,
∵∠B=50°,
∴∠DFB=$\frac{1}{2}×(180°-50°)$=65°;
(2)理由是:∵DE∥AB,
∴∠FDE=∠BFD,
∵∠A=∠FDE,
∴∠A=∠BFD,
∴DF∥AC.
点评 本题考查了平行线的性质和判定定理,能灵活运用平行线的判定和性质定理进行推理是解此题的关键.

练习册系列答案
相关题目
12.下列四个点,在正比例函数y=$\frac{2}{5}$x的图象上的点是( )
| A. | (2,5) | B. | (5,2) | C. | (2,-5) | D. | (5,-2) |
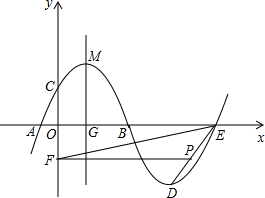 如图,抛物线m:y=-0.25(x+h)2+k与x轴的交点为A,B,与y轴的交点为C,顶点为M(3,6.25),将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D.
如图,抛物线m:y=-0.25(x+h)2+k与x轴的交点为A,B,与y轴的交点为C,顶点为M(3,6.25),将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D.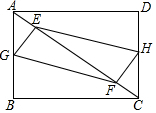 如图,在矩形ABCD中,AB=3cm,BC=4cm,E、F是对角线AC上的两个动点,分别从A、C同时出发相向而行,速度均为1cm/秒,运动时间为t秒,当其中一个动点到达后就停止运动.
如图,在矩形ABCD中,AB=3cm,BC=4cm,E、F是对角线AC上的两个动点,分别从A、C同时出发相向而行,速度均为1cm/秒,运动时间为t秒,当其中一个动点到达后就停止运动. 如图,AB∥CD∥EF,写出∠B、∠D、∠BED之间的数量关系,并说明理由.
如图,AB∥CD∥EF,写出∠B、∠D、∠BED之间的数量关系,并说明理由.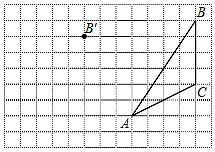 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC平移后得到△A′B′C′,图中点B′为点B的对应点.
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC平移后得到△A′B′C′,图中点B′为点B的对应点.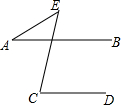 如图所示,已知AB∥CD,∠C=75°,∠A=25°,求∠E的度数.
如图所示,已知AB∥CD,∠C=75°,∠A=25°,求∠E的度数.