题目内容
9.已知某函数图象经过点(-1,1),且当x>0时,y随x的增大而增大.请你写出一个满足条件的函数解析式:y=x+2(答案不唯一).分析 根据该函数的增减性确定其比例系数的取值,然后代入已知点后即可求得其解析式.
解答 解:∵当x>0时,y随x的增大而增大,
∴设解析式为:y=x+b,
∵图象经过点(-1,1),
∴1=-1+b,
解得:b=2;
∴解析式为:y=x+2(答案不唯一).
故答案为x+2(答案不唯一).
点评 本题考查了函数的性质,用到的知识点:函数图象经过点,则点的坐标满足函数解析式;一次函数y=kx+b(k≠0)中,当k>0时,y随x的增大而增大,k<0时,y随x的增大而减小.本题是开放性试题,答案不唯一,也可以举反比例函数或二次函数的例子.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.在某中学开展的“书香伴我行”读书活动中,为了解九年级300名学生读书情况,随机调查了九年级50名学生读书的册数.统计数据如下表所示:
①这50个样本数据的众数是3,中位数是2.
②根据样本数据,估计该校九年级300名学生在本次活动中读书多于2册的人数;
③学校广播站的小记者对被调查的50名学生中读书册数最少和最多的人进行随即采,请利用树状图或列表,求被采访的两人恰好都是读书册数最多的学生的概率.
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 13 | 16 | 17 | 3 |
②根据样本数据,估计该校九年级300名学生在本次活动中读书多于2册的人数;
③学校广播站的小记者对被调查的50名学生中读书册数最少和最多的人进行随即采,请利用树状图或列表,求被采访的两人恰好都是读书册数最多的学生的概率.
17.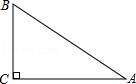 如图,已知斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,则斜坡AB的长为( )
如图,已知斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,则斜坡AB的长为( )
 如图,已知斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,则斜坡AB的长为( )
如图,已知斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,则斜坡AB的长为( )| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{5}$ | C. | 18 | D. | 8$\sqrt{3}$ |
4.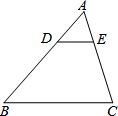 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{9}$ |
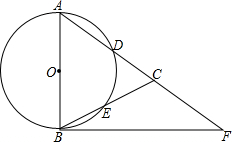 如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且BF是⊙O的切线.
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且BF是⊙O的切线. 甲骑车到乙家研讨数学问题,中途因等候红灯停止了一分钟,之后又骑行了1.2千米到达了乙家.若甲骑行的速度始终不变,从出发开始计时,剩余的路程S(单位:千米)与时间t(单位:分钟)的函数关系的图象如图所示,则图中a等于( )
甲骑车到乙家研讨数学问题,中途因等候红灯停止了一分钟,之后又骑行了1.2千米到达了乙家.若甲骑行的速度始终不变,从出发开始计时,剩余的路程S(单位:千米)与时间t(单位:分钟)的函数关系的图象如图所示,则图中a等于( )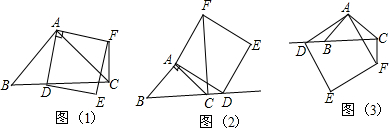
 如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.