题目内容
17.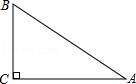 如图,已知斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,则斜坡AB的长为( )
如图,已知斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,则斜坡AB的长为( )| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{5}$ | C. | 18 | D. | 8$\sqrt{3}$ |
分析 首先根据斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,可得AC=8米,BC=4米,然后利用勾股定理求出AB的长度.
解答 解:∵斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,
∴AC=8米,BC=4米,
则AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$(米).
故选B.
点评 本题考查了解直角三角形的应用-坡度坡角问题,解答本题的关键是正确理解坡度的定义,坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度.也考查了勾股定理.

练习册系列答案
相关题目
8. 已知某几何体的三视图如图所示,则该几何体是( )
已知某几何体的三视图如图所示,则该几何体是( )
 已知某几何体的三视图如图所示,则该几何体是( )
已知某几何体的三视图如图所示,则该几何体是( )| A. | 圆柱 | B. | 棱柱 | C. | 圆锥 | D. | 三棱锥 |
5.下列计算正确的是( )
| A. | 2a-a=1 | B. | a2+a2=2a4 | C. | a2•a3=a5 | D. | (a-b)2=a2-b2 |
6. 如图所示的工件的俯视图是( )
如图所示的工件的俯视图是( )
 如图所示的工件的俯视图是( )
如图所示的工件的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
7.分式$\frac{{{x^2}-9}}{x+3}$的值为0,则x的值为( )
| A. | -3 | B. | 3 | C. | 0 | D. | ±3 |
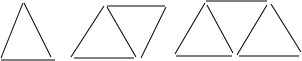 用牙签按下图的方式搭三角形,搭n个这样的三角形需要2n+1根牙签.
用牙签按下图的方式搭三角形,搭n个这样的三角形需要2n+1根牙签. 如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上,第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2014次跳2014步就跳到了( )号位置上.
如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上,第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2014次跳2014步就跳到了( )号位置上.