题目内容
19.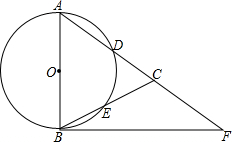 如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且BF是⊙O的切线.
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且BF是⊙O的切线.(1)求证:∠BAC=2∠CBF;
(2)若⊙O的半径为5,sin∠CBF=$\frac{2}{5}$,求CD的长.
分析 (1)连接AD,根据圆周角的性质求得AE⊥BC,根据等腰三角形的性质三效合一的性质得出∠BAE=∠CAE=$\frac{1}{2}∠$BAC,然后根据弦切角定理得出∠CBF=∠BAE=$\frac{1}{2}∠BAC$;
(2)连接BD,由⊙O的半径为5,解出AC=AB=10,根据勾股定理求出BC=2BE=8,在根据勾股定理列方程求解.
解答  (1)如图1,证明;连接AE,
(1)如图1,证明;连接AE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵AB=AC,
∴∠BAE=∠CAE=$\frac{1}{2}$∠BAC,
∵BF是⊙O的切线,
∴∠CBF-∠BAE=$\frac{1}{2}$∠BAC,
∴∠BAC=2∠CBF;
(2)解:如图2,连接BD,
∵AB=AC=2OB=10,
∵sin∠CBF=$\frac{2}{5}$,
∴∠BAE=$\frac{2}{5}$,
∴BE=4,
∴BC=2BE=8,
设CD=x,则AD=10-x,
∵AB是⊙O的直径,
∴∠BAD=90°,
∴∠BCD=90°,
∴82-x2=102-(10-x)2,
解得:x=$\frac{16}{5}$,
∴CD=$\frac{16}{5}$.
点评 本题考查了圆的切线的判定定理、圆周角定理、等腰三角形的性质、勾股定理弦切角定理,解题的关键是作出辅助线构造直角三角形.

练习册系列答案
相关题目
15.某水果市场上的苹果的价格如下:
甲、乙两组共买了100kg苹果,甲组比乙组少花38元,问甲组比乙组少买多少苹果?
| 购买苹果数量 | 不超过30千克 | 超30千克但不超过50千克 | 50千克以上 |
| 每千克价格/元 | 3元 | 2.5元 | 2元 |
11.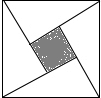 由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )
由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )
 由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )
由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )| A. | 1 | B. | 3 | C. | 4-2$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
8. 已知某几何体的三视图如图所示,则该几何体是( )
已知某几何体的三视图如图所示,则该几何体是( )
 已知某几何体的三视图如图所示,则该几何体是( )
已知某几何体的三视图如图所示,则该几何体是( )| A. | 圆柱 | B. | 棱柱 | C. | 圆锥 | D. | 三棱锥 |
 如图,△ABC≌△FED且BC=DE,问AB∥EF吗?请说明理由.
如图,△ABC≌△FED且BC=DE,问AB∥EF吗?请说明理由.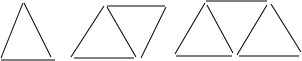 用牙签按下图的方式搭三角形,搭n个这样的三角形需要2n+1根牙签.
用牙签按下图的方式搭三角形,搭n个这样的三角形需要2n+1根牙签.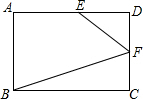 已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF,若AB=4,BC=5,则AE=$\frac{29}{10}$.
已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF,若AB=4,BC=5,则AE=$\frac{29}{10}$.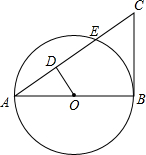 如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.
如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.