题目内容
4.设P=$\frac{{{2^{2013}}+1}}{{{2^{2014}}+1}}$,Q=$\frac{{{2^{2014}}+1}}{{{2^{2015}}+1}}$,则P与Q的大小关系是( )| A. | P>Q | B. | P=Q | C. | P<Q | D. | 不能确定 |
分析 根据作差法,可得分式的加减,根据通分,可得同分母分式的加减,根据同底数幂的乘法,可得答案.
解答 解:P-Q=$\frac{{2}^{2013}+1}{{2}^{2014}+1}$-$\frac{{2}^{2014}+1}{{2}^{2015}+1}$
=$\frac{{2}^{2013+2015}+{2}^{2013}+{2}^{2015}+1}{({2}^{2014}+1)({2}^{2015}+1)}$-$\frac{{2}^{201+2014}+{2}^{2014}+{2}^{2014}+1}{({2}^{2014}+1)({2}^{2015}+1)}$
=$\frac{{2}^{2013}+{2}^{2015}-2×{2}^{2014}}{({2}^{2014}+1)({2}^{2015}+1)}$
=$\frac{{2}^{2013}}{({2}^{2014}+1)({2}^{2015}+1)}$>0,
P>Q.
故选:A.
点评 本题考查了分式的加减法,作差法是两数大小的常用方法:差大于零,被减数大于减数;差等于零,两数一样大;差小于零,被减数小于减数.

练习册系列答案
相关题目
14.方程组$\left\{\begin{array}{l}x-y=3\\ 2x+y=6\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=3\\ y=0\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=6\\ y=1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=6\\ y=-1\end{array}\right.$ |
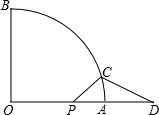 如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.
如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.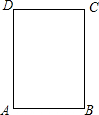 如图,在长方形ABCD中,AB=3cm,BC=4cm,点P延边按A→B→C→D的方向运动到点D(但不与A,B两点重合),求APD的面积y(cm2)与点P所行的路程x(cm)之间的函数关系式.
如图,在长方形ABCD中,AB=3cm,BC=4cm,点P延边按A→B→C→D的方向运动到点D(但不与A,B两点重合),求APD的面积y(cm2)与点P所行的路程x(cm)之间的函数关系式.