题目内容
9.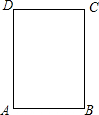 如图,在长方形ABCD中,AB=3cm,BC=4cm,点P延边按A→B→C→D的方向运动到点D(但不与A,B两点重合),求APD的面积y(cm2)与点P所行的路程x(cm)之间的函数关系式.
如图,在长方形ABCD中,AB=3cm,BC=4cm,点P延边按A→B→C→D的方向运动到点D(但不与A,B两点重合),求APD的面积y(cm2)与点P所行的路程x(cm)之间的函数关系式.
分析 分三种情形当点P在AB上,②当点P在CB上,③当点P在CD上,确定自变量取值范围后,根据三角形面积公式计算即可.
解答 解:∵四边形ABCD是矩形,
∴AD=BC=4,AB=CD=3,
① 当点P在AB上时,即0<x≤3时,y=$\frac{1}{2}$•4•x=2x.
当点P在AB上时,即0<x≤3时,y=$\frac{1}{2}$•4•x=2x.
②当点P在CB上时,即3<x≤7时,y=$\frac{1}{2}$•4•3=6.
③当点P在CD上时,即7<x<10时,y=$\frac{1}{2}$•4•(10-x)=-2x+20.
综上所述y=$\left\{\begin{array}{l}{2x}&{(0<x≤3)}\\{6}&{(3<x≤7)}\\{-2x+20}&{(7<x<10)}\end{array}\right.$.
点评 本题考查动点问题的函数图象、矩形的性质、三角形的面积公式等知识,解题的关键是学会分类讨论的思想方法,属于中考常考题型.

练习册系列答案
相关题目
17.下列图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.设P=$\frac{{{2^{2013}}+1}}{{{2^{2014}}+1}}$,Q=$\frac{{{2^{2014}}+1}}{{{2^{2015}}+1}}$,则P与Q的大小关系是( )
| A. | P>Q | B. | P=Q | C. | P<Q | D. | 不能确定 |
18.下列运算正确的是( )
| A. | 3a2-a=2a | B. | a-(1-2a)=a-1 | C. | -5(1-a2)=-5-5a2 | D. | a3+7a3-5a3=3a3 |
19.如果A(1-a,b+1)关于y轴的对称点在第三象限,那么点B(1-a,b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第6块.
如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第6块.