题目内容
17.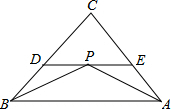 如图,△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC、AC于点D、E.
如图,△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC、AC于点D、E.(1)如果∠C=80°,求∠BPA的度数.
(2)求证:DE=BD+AE.
分析 (1)根据三角形的内角和定理求出∠ABC+∠CAB,再根据角平分线的定义求出∠PBC+∠PAB,然后利用三角形的内角和定理列式计算即可得解.
(2)先根据角平分线的定义及平行线的性质证明△BDP和△AEP是等腰三角形,再由等腰三角形的性质得BD=DP,AE=EP,于是得到结论.
解答 解:(1)∵∠ABC+∠C+∠CAB=180°,∠C=80°,
∴∠ABC+∠CAB=100°.
∵∠ABC,∠CAB的平分线交于点P,
∴∠PBA=$\frac{1}{2}$∠ABC,∠PAB=$\frac{1}{2}$∠CAB.
∴∠PBC+∠PAB=$\frac{1}{2}$(∠CBA+∠CAB)=50°.
∵∠PBA+∠PAB+∠BPA=180°,
∴∠BPA=180°-50°=130°;
(2)证明:∵BP平分∠CBA,
∴∠DBP=∠ABP,
∵DE∥AB,
∴∠DPB=∠ABP,
∴∠DBP=∠DPB,
∴BD=PD,
同理可得PE=EA,
∴DE=DP+PE=BD+AE.
点评 本题考查三角形的内角和定理,等腰三角形的性质,平行线的性质及角平分线的性质,整体思想的利用和有效的进行线段的等量代换是正确解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 一副三角板按如图所示的方式摆放,且∠1的度数是∠2的3倍,则∠2的度数为( )
一副三角板按如图所示的方式摆放,且∠1的度数是∠2的3倍,则∠2的度数为( )
 一副三角板按如图所示的方式摆放,且∠1的度数是∠2的3倍,则∠2的度数为( )
一副三角板按如图所示的方式摆放,且∠1的度数是∠2的3倍,则∠2的度数为( )| A. | 20° | B. | 22.5° | C. | 25° | D. | 67.5° |
9.下列运算错误的是( )
| A. | 2b+5b=7b | B. | (b2)5=b10 | C. | b2•b3=b7 | D. | b9÷b3=b3 |
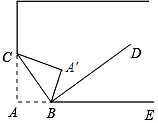 如图,将书角斜折过去,使角顶点落在A′处,BC为折痕,∠A′BD=∠DBE,求∠CBD的度数.
如图,将书角斜折过去,使角顶点落在A′处,BC为折痕,∠A′BD=∠DBE,求∠CBD的度数.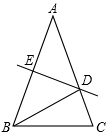 如图,在△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB、AC于E、D两点.
如图,在△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB、AC于E、D两点.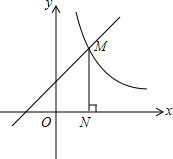 如图,一次函数y=x+1的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1.
如图,一次函数y=x+1的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1.