题目内容
6.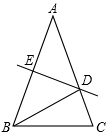 如图,在△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB、AC于E、D两点.
如图,在△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB、AC于E、D两点.(1)若△BCD的周长为8,求BC的长;
(2)若∠ABD:∠DBC=1:3,求∠A的度数.
分析 (1)根据线段垂直平分线定理得出AD=BD,根据BC+CD+BD=8求出AC+BC=8,把AC的长代入求出即可;
(2)根据三角形的内角和列方程即可得到结论.
解答 解:(1)∵D在AB垂直平分线上,
∴AD=BD,
∵△BCD的周长为8,
∴BC+CD+BD=8,
∴AD+DC+BC=8,
∴AC+BC=8,
∵AB=AC=5,
∴BC=8-5=3;
(2)设∠A=x,则∠ABC=∠ACB=4x,
∴x+4x+4x=180°,
解得:x=20°,
∴∠A=20°.
点评 本题考查了等腰三角形性质和线段垂直平分线定理,关键是求出AC+BC的值,注意:线段垂直平分线上的点到线段的两端点的距离相等.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
16.如果a+b=c,且a、b都大于c,那么a、b一定是( )
| A. | 同为负数 | B. | 一个正数一个负数 | ||
| C. | 同为正数 | D. | 一个负数一个是零 |
11. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)若点(x1,y1),(x2,y2)在图象上,当x2>x1>0时,y2>y1;
(2)当x<-1时,y>0;
(3)4a+2b+c>0;
(4)x=3是关于x方程ax2+bx+c=0的一个根,其中正确的个数为( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:(1)若点(x1,y1),(x2,y2)在图象上,当x2>x1>0时,y2>y1;
(2)当x<-1时,y>0;
(3)4a+2b+c>0;
(4)x=3是关于x方程ax2+bx+c=0的一个根,其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.-2015的倒数是( )
| A. | 2015 | B. | -$\frac{1}{2015}$ | C. | $\frac{1}{2015}$ | D. | -2015 |
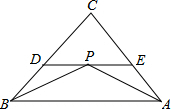 如图,△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC、AC于点D、E.
如图,△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC、AC于点D、E. 如图,已知反比例函数y=$\frac{2}{x}$的图象上有一组点B1,B2,…Bn,它们的横坐标依次增加1,且点B1横坐标为1.“①,②,③…”分别表示如图所示的三角形的面积,记S1=①-②,S2=②-③,…,S1+S2+…+Sn=$\frac{n}{n+1}$(用含n的式子表示).
如图,已知反比例函数y=$\frac{2}{x}$的图象上有一组点B1,B2,…Bn,它们的横坐标依次增加1,且点B1横坐标为1.“①,②,③…”分别表示如图所示的三角形的面积,记S1=①-②,S2=②-③,…,S1+S2+…+Sn=$\frac{n}{n+1}$(用含n的式子表示).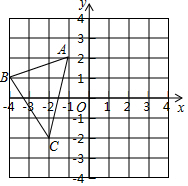 如图,已知△ABC的三个顶点的坐标为A(-1,2),B(-4,1),C(-2,-2).
如图,已知△ABC的三个顶点的坐标为A(-1,2),B(-4,1),C(-2,-2).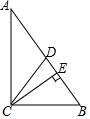 如图,在△ABC中,∠ACB=90°,CD是AB边上的中线,CE⊥AB于E,AC=8,BC=6,则DE=1.4.
如图,在△ABC中,∠ACB=90°,CD是AB边上的中线,CE⊥AB于E,AC=8,BC=6,则DE=1.4. 如下数表是由从1开始的连续自然数组成的,则第10行各数之和1729.
如下数表是由从1开始的连续自然数组成的,则第10行各数之和1729.