题目内容
如图，已知△ABC中，AB＞AC，AD是BC边上的高，求证：AB2-AC2=BC（BD-DC）考点：勾股定理
专题：证明题
分析：先根据勾股定理得出AB2=AD2+BD2，AC2=AD2+CD2，再把两式相减即可．
解答：证明：∵AD是BC边上的高，
∴AB2=AD2+BD2，AC2=AD2+CD2，
∴AB2-AC2=AD2+BD2-AD2-CD2=BD2-CD2=（BD+CD）（BD-CD）=BC•（BD-CD）．
∴AB2=AD2+BD2，AC2=AD2+CD2，
∴AB2-AC2=AD2+BD2-AD2-CD2=BD2-CD2=（BD+CD）（BD-CD）=BC•（BD-CD）．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知二次函数图象经过点（1，-3）、（-1，1）、（0，-2）．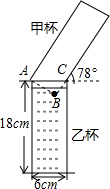
如图，有两个高度相等且底面直径不等的圆柱形水杯，中杯转满液体，乙杯是空杯，若把甲杯中的液体全部倒人乙杯，则乙杯中的液面与图中点B的距离约为多少？（结果精确到0.01cm，参考数据：sin78°≈0.98，cos78°≈0.21，tan78°≈4.70）
要焊接一个如图所示的钢架，大约需要多少米的钢材（精确到0.1m）？（图中的△BCE和△ABD都是等腰直角三角形，CD=8m，BE=3m）若一元二次方程9x2-12x-39996=0的两根为a，b，且a＜b，则a+3b的值为（ ）
| A、136 | ||
| B、268 | ||
C、
| ||
D、
|