题目内容
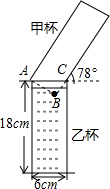如图，有两个高度相等且底面直径不等的圆柱形水杯，中杯转满液体，乙杯是空杯，若把甲杯中的液体全部倒人乙杯，则乙杯中的液面与图中点B的距离约为多少？（结果精确到0.01cm，参考数据：sin78°≈0.98，cos78°≈0.21，tan78°≈4.70）考点：解直角三角形的应用
专题：
分析：根据题意首先得出甲杯的底面直径，进而求出乙杯中液体的高度，即可得出答案．
解答：解：由题意可得：AC=6cm，则sin∠ACB=
，
故AB=AC•sin∠ACB=6×0.98=5.88（cm），
设乙杯中液体的高度为hcm，
则π×（5.88÷2）2×18=h×π×32，
解得：h≈17.29，
故乙杯中的液面与图中点B的距离约为：18-17.29=0.71（cm）．
| AB |
| AC |
故AB=AC•sin∠ACB=6×0.98=5.88（cm），
设乙杯中液体的高度为hcm，
则π×（5.88÷2）2×18=h×π×32，
解得：h≈17.29，
故乙杯中的液面与图中点B的距离约为：18-17.29=0.71（cm）．
点评：此题主要考查了解直角三角形的应用，根据题意得出AB的长是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，将4个直角边长为1和
如图，已知△ABC中，AB＞AC，AD是BC边上的高，求证：AB2-AC2=BC（BD-DC）
已知点A（2，-2），如果把点A向上平移4个单位，再向左平移4个单位得到点C，那么C点的坐标是（ ）
| A、（-2，2） |
| B、（2，2） |
| C、（-1，-1） |
| D、（-2，-2） |
下列四个有理数
、0、1、-2，任取两个相乘，积最小为（ ）
| 1 |
| 2 |
A、
| ||
| B、0 | ||
| C、-1 | ||
| D、-2 |