Question

3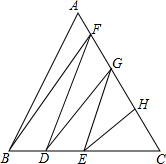．如图所示，等边三角形ABC的边长是100cm，用折线把这个等边三角形分割成面积相等的六个三角形，那么图中CD+CG的长是多少？

Answer 1

分析 根据三角形ABC的边长都是100厘米，用折线把三角形分割成面积相等的六个三角形，可得△ABF和△BFC的面积之比是1：5，根据三角形的高一定时，面积与底成正比的性质可得：AF：FC=1：5；因为AC=100厘米，即可求得FC=100×$\frac{5}{6}$=$\frac{100}{3}$厘米；同理即可求得CD和CG的长度．

解答 解：根据题干可得：S_△ABF=S_△BDF=S_△DGF=S_△DEG=S_△GEH=S_△EHC，
（1）△ABF和△BFC的面积之比是1：5，根据三角形的高一定时，面积与底成正比的性质可得：AF：FC=1：5；因为AC=100厘米，即可求得CF=100×$\frac{5}{6}=\frac{100}{3}$厘米；
（2）△DBF和△DFC的面积之比是1：4，根据三角形的高一定时，面积与底成正比的性质可得：DB：DC=1：4；因为BC=100厘米，即可求得DC=100×$\frac{3}{4}$=75厘米；
（3）△FDG和△DGC的面积之比是1：3，根据三角形的高一定时，面积与底成正比的性质可得：FG：GC=1：3；因为FC=$\frac{100}{3}$厘米，即可求得CG=$\frac{100}{3}$×$\frac{3}{4}$=25厘米；
25+75=100（厘米），
答：CD和CG的长度和是100厘米．

点评 此题反复考查了三角形的高一定时，三角形的面积与底成正比的性质的灵活应用，根据三角形的高一定时，面积与底成正比的性质解答是关键．