题目内容
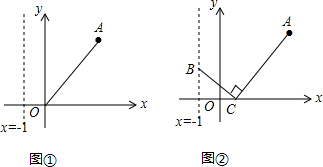
15.已知点A(3,4),点B为直线x=-1上的动点,设B(-1,y).(1)如图①,若△ABO是等腰三角形且AO=AB时,求点B的坐标;
(2)如图②,若点C(x,0)且-1<x<3,BC⊥AC垂足为点C;
①当x=0时,求tan∠BAC的值;
②若AB与y轴正半轴的所夹锐角为α,当点C在什么位置时tanα的值最大?
分析 (1)在Rt△ABE中,根据勾股定理得到AE2+BE2=AB2,即可得到结论;
(2)①由点C(x,0),当x=0时,点C与O重合,如图②,设直线x=-1与x轴交于G,过A作AF⊥x轴于F,通过△AOF∽△OBG,得到BO:AO=OG:AF=1:4,于是得到tan∠BAC=$\frac{1}{4}$,②设直线x=-1与x轴交于G,过A作AH⊥直线x=-1于H,AF⊥x轴于F,根据平行线的性质得到∠ABH=α,由三角函数的定义得到tanα=$\frac{4}{BH}$,根据相似三角形的性质得到比例式$\frac{y}{x-3}=\frac{x+1}{4}$,于是得到y=-$\frac{1}{4}$(x+1)(3-x)=-$\frac{1}{4}$(x-1)2+1,根据二次函数的性质即可得到结论.
解答 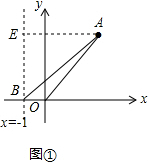 解:(1)如图①,过A作AE⊥直线x=-1于E,
解:(1)如图①,过A作AE⊥直线x=-1于E,
在Rt△ABE中,
∵AE2+BE2=AB2,
∴(4-y)2+42=52;
解得y=1或7,
∴B(-1,1)或B(-1,7);
(2)①∵点C(x,0),当x=0时,点C与O重合,如图②,设直线x=-1与x轴交于G,过A作AF⊥x轴于F,
∴∠BGO=∠AOB=∠AFO=90°,
∴∠GBO+∠BOG=∠BOG+∠AOF=90°,
∴∠GBO=∠AOF,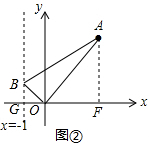
∴△AOF∽△OBG,
∴BO:AO=OG:AF=1:4,
∴tan∠BAC=$\frac{1}{4}$,
②如图③,设直线x=-1与x轴交于G,过A作AH⊥直线x=-1于H,AF⊥x轴于F,
∵BE∥y轴,
∴∠ABH=α,
在Rt△ABE中,tanα=$\frac{4}{BH}$,
∵tanα随BH的增大而减小,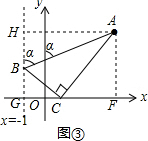
∴当BH最小时tanα有最大值;即BG最大时,tanα有最大值,
由(1)证得△ACF∽△CBG,
∴$\frac{BG}{CF}=\frac{CG}{AF}$,即$\frac{y}{x-3}=\frac{x+1}{4}$,
∴y=-$\frac{1}{4}$(x+1)(3-x)=-$\frac{1}{4}$(x-1)2+1,
当x=1时,ymax=1,
即当C(1,0)时,tanα有最大值$\frac{4}{3}$.
点评 本题考查了相似三角形的判定和性质,三角函数的定义,平行线的性质,勾股定理,正确的作出辅助线证得△ACF∽△CBG是解题的关键.

| A. | 2 | B. | 4 | C. | ±2 | D. | ±4 |
| A. | $\sqrt{18a}$ | B. | $\sqrt{{a}^{2}+{b}^{2}}$ | C. | $\sqrt{{x}^{3}y}$ | D. | $\sqrt{\frac{12}{5}}$ |
 某中学建了一座竖直的电子屏幕HG,它的底部G点到地面BF的距离为3米,小明在CD处看电子屏幕的底部G点的仰角为30°,他在此处觉得视角不好,然后他后退了2米到AB处觉得好多了,此时他看电子屏幕的顶部H点的仰角为45°,已知小明眼睛到地面的距离为1.5米,求电子屏幕的宽度HG(结果精确到0.1,参考数据$\sqrt{2}≈$1.41,$\sqrt{3}$≈1.73)
某中学建了一座竖直的电子屏幕HG,它的底部G点到地面BF的距离为3米,小明在CD处看电子屏幕的底部G点的仰角为30°,他在此处觉得视角不好,然后他后退了2米到AB处觉得好多了,此时他看电子屏幕的顶部H点的仰角为45°,已知小明眼睛到地面的距离为1.5米,求电子屏幕的宽度HG(结果精确到0.1,参考数据$\sqrt{2}≈$1.41,$\sqrt{3}$≈1.73)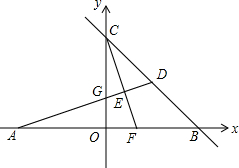 如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.
如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.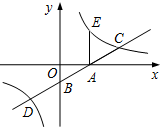 如图,直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x,y轴分别交于点A,B,与反比例函数y=$\frac{k}{x}$(k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
如图,直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x,y轴分别交于点A,B,与反比例函数y=$\frac{k}{x}$(k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.