题目内容
14. 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P是切点,AB=12$\sqrt{3}$,OP=6,则大圆的半径长为( )
如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P是切点,AB=12$\sqrt{3}$,OP=6,则大圆的半径长为( )| A. | 6 | B. | 6$\sqrt{3}$ | C. | 6$\sqrt{2}$ | D. | 12 |
分析 连接OA,由切线的性质可知OP⊥AB,由垂径定理可知AP=PB,在Rt△OAP中,利用勾股定理可求得OA的长.
解答  解:
解:
如图,连接OA,
∵AB是小圆的切线,
∴OP⊥AB,
∵OP过圆心,
∴AP=BP=$\frac{1}{2}$AB=6$\sqrt{3}$,
在Rt△AOP中,由勾股定理可得OA=$\sqrt{A{P}^{2}+O{P}^{2}}$=$\sqrt{(6\sqrt{3})^{2}+{6}^{2}}$=12,
即大圆的半径为12,
故选D.
点评 本题主要考查切线的性质,由切线的性质及垂径定理构造直角三角形是解题的关键.

练习册系列答案
相关题目
 如图是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.建立平面直角坐标系,则抛物线的关系式是y=-$\frac{1}{2}$x2.
如图是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.建立平面直角坐标系,则抛物线的关系式是y=-$\frac{1}{2}$x2. 如图:在直角坐标系中,O是坐标原点,已知A(4,3),P是坐标轴上的一点,若以O、A、P三点组成的三角形为等腰三角形,则满足条件的点P共有8个,写出其中一个点P的坐标是(5,0)(答案不唯一).
如图:在直角坐标系中,O是坐标原点,已知A(4,3),P是坐标轴上的一点,若以O、A、P三点组成的三角形为等腰三角形,则满足条件的点P共有8个,写出其中一个点P的坐标是(5,0)(答案不唯一). 如图,两圆相交于点P、Q,大圆的割线AD交小圆于点B、C,求证:∠APB+∠CQD=180°.
如图,两圆相交于点P、Q,大圆的割线AD交小圆于点B、C,求证:∠APB+∠CQD=180°.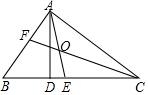 如图,在△ABC中,∠BAC=90°,∠B=50°,AE,CF是角平分线,它们相交于为O,AD是高,求∠BAD和∠AOC的度数.
如图,在△ABC中,∠BAC=90°,∠B=50°,AE,CF是角平分线,它们相交于为O,AD是高,求∠BAD和∠AOC的度数.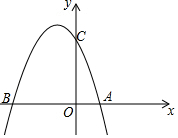 已知抛物线y=ax2+bx+3(a≠0)交x轴于A(1,0)和B (-3,0),交y轴于C.
已知抛物线y=ax2+bx+3(a≠0)交x轴于A(1,0)和B (-3,0),交y轴于C.