题目内容
9.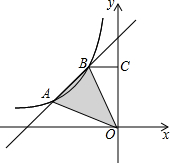 如图,直线y=x+4与双曲线y=$\frac{k}{x}$(x<0)交于点A、B,过点B向y轴作垂线,垂足为C,若BC=$\frac{1}{2}$AB,△AOB的面积为3,则k值为-3$\sqrt{2}$+$\frac{9}{8}$.
如图,直线y=x+4与双曲线y=$\frac{k}{x}$(x<0)交于点A、B,过点B向y轴作垂线,垂足为C,若BC=$\frac{1}{2}$AB,△AOB的面积为3,则k值为-3$\sqrt{2}$+$\frac{9}{8}$.
分析 设直线AB与x轴交于M,与y轴交于N,过O作OD⊥AB于D,得到M(-4,0),N(0,4),求得OM=ON=4,推出△MON是等腰直角三角形,根据三角形的面积得到AB=$\frac{3\sqrt{2}}{2}$,得到BC=$\frac{3\sqrt{2}}{4}$,得到B(-$\frac{3\sqrt{2}}{4}$,$\frac{16-3\sqrt{2}}{4}$),于是得到结论.
解答 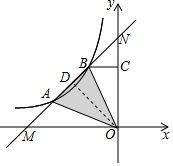 解:设直线AB与x轴交于M,与y轴交于N,
解:设直线AB与x轴交于M,与y轴交于N,
过O作OD⊥AB于D,
在y=x+4中,令x=0,则y=4,令y=0,则x=-4,
∴M(-4,0),N(0,4),
∴OM=ON=4,
∴△MON是等腰直角三角形,
∴OD=$\frac{1}{2}$MN=2$\sqrt{2}$,
∵△AOB的面积为3,
∴AB=$\frac{3\sqrt{2}}{2}$,
∵BC=$\frac{1}{2}$AB,
∴BC=$\frac{3\sqrt{2}}{4}$,
∵BC⊥y轴,
∴CN=BC=$\frac{3\sqrt{2}}{4}$,
∴OC=ON-CN=$\frac{16-3\sqrt{2}}{4}$,
∴B(-$\frac{3\sqrt{2}}{4}$,$\frac{16-3\sqrt{2}}{4}$),
∴k=(-$\frac{3\sqrt{2}}{4}$)×$\frac{16-3\sqrt{2}}{4}$=-3$\sqrt{2}$+$\frac{9}{8}$.
故答案为:-3$\sqrt{2}$+$\frac{9}{8}$.
点评 本题考查了一次函数与反比例函数的交点问题,等腰直角三角形的性质,三角形面积的计算,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
20.观察下表:
我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
(1)第3格的“特征多项式”为16x+9y,第4格的“特征多项式”为25x+16y,第n格的“特征多项式”为(n+1)2x+n2y;
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16.
①求x,y的值;
②在①的条件下,第n格的“特征多项式”是否有最小值?若有,求出最小值和相应的n值;若没有,请说明理由.
我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x y y y x x x x | … |
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16.
①求x,y的值;
②在①的条件下,第n格的“特征多项式”是否有最小值?若有,求出最小值和相应的n值;若没有,请说明理由.
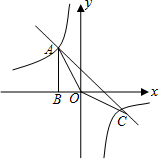 如图,点A(-1,m)是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点,另一个交点C在第四象限,AB⊥x轴于B,且cos∠AOB=$\frac{\sqrt{10}}{10}$
如图,点A(-1,m)是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点,另一个交点C在第四象限,AB⊥x轴于B,且cos∠AOB=$\frac{\sqrt{10}}{10}$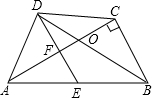 在四边形ABCD中,BD平分∠ABC,E为AB的中点,DE∥CB,∠ACB=90°,下面的结论中,正确的有①③④.①△BDE为等腰三角形,②∠AED=∠AOD,③AO•OC=DO•OB,④∠CAB=30°时,四边形BCDE为菱形.
在四边形ABCD中,BD平分∠ABC,E为AB的中点,DE∥CB,∠ACB=90°,下面的结论中,正确的有①③④.①△BDE为等腰三角形,②∠AED=∠AOD,③AO•OC=DO•OB,④∠CAB=30°时,四边形BCDE为菱形.