题目内容
3.连接多边形任意两个不相邻顶点的线段称为多边形的对角线.(1)
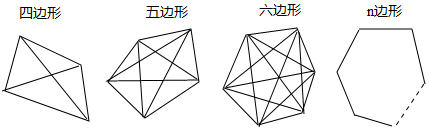
对角线条数分别为2、5、9、$\frac{n(n-3)}{2}$.
(2)n边形可以有20条对角线吗?如果可以,求边数n的值;如果不可以,请说明理由.
(3)若一个n边形的内角和为1800°,求它对角线的条数.
分析 (1)设n边形的对角线条数为an,根据多边形对角线条数公式即可求出结论;
(2)假设可以,根据多边形对角线条数公式,可得出关于n的一元二次方程,解之即可得出结论;
(3)根据多边形内角和定理,可求出边数,再套用多边形对角线条数公式,即可得出结论.
解答 解:(1)设n边形的对角线条数为an,
则a4=$\frac{4×(4-3)}{2}$=2,a5=$\frac{5×(5-3)}{2}$=5,a6=$\frac{6×(6-3)}{2}$=9,…,an=$\frac{n(n-3)}{2}$.
故答案为:2;5;9;$\frac{n(n-3)}{2}$.
(2)假设可以,根据题意得:
$\frac{n(n-3)}{2}$=20,
解得:n=8或n=-5(舍去),
∴n边形可以有20条对角线,此时边数n为八.
(3)∵一个n边形的内角和为1800°,
∴180°×(n-2)=1800°,
解得:n=12,
∴$\frac{n(n-3)}{2}$=$\frac{12×(12-2)}{2}$=60.
答:这个多边形有60条对角线.
点评 本题考查了一元二次方程的应用、多边形的对角线以及多边形内角和定理,解题的关键是:(1)根据多边形对角线条数公式求出多边形的对角线条数;(2)根据多边形对角线条数公式,列出关于n的一元二次方程;(3)根据多边形内角和定理,求出边数n.

练习册系列答案
相关题目
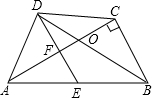 在四边形ABCD中,BD平分∠ABC,E为AB的中点,DE∥CB,∠ACB=90°,下面的结论中,正确的有①③④.①△BDE为等腰三角形,②∠AED=∠AOD,③AO•OC=DO•OB,④∠CAB=30°时,四边形BCDE为菱形.
在四边形ABCD中,BD平分∠ABC,E为AB的中点,DE∥CB,∠ACB=90°,下面的结论中,正确的有①③④.①△BDE为等腰三角形,②∠AED=∠AOD,③AO•OC=DO•OB,④∠CAB=30°时,四边形BCDE为菱形.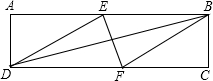 如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题: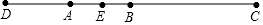 已知线段AB,在AB的延长线上取一点C,使BC=2AB,在BA的延长线上取一点D,使DA=AB,取AB中点E,若DE=7.5cm,求DC的长.
已知线段AB,在AB的延长线上取一点C,使BC=2AB,在BA的延长线上取一点D,使DA=AB,取AB中点E,若DE=7.5cm,求DC的长.