题目内容
12.在公式S=v0t+$\frac{1}{2}$at2中,当t=2时,S=18;当t=-2时,S=10.则t=1时,S=$\frac{11}{2}$.分析 把t与S两对值代入公式计算求出V0,a的值,确定出公式,将t=3代入计算即可求出S的值.
解答 解:把t=2,S=18;t=-2,S=10代入得:$\left\{\begin{array}{l}{2{v}_{0}+2a=18}\\{-2{v}_{0}+2a=10}\end{array}\right.$,
解得:a=7,V0=2,
∴S=2t+$\frac{7}{2}$t2,
把t=1代入得:S=2+$\frac{7}{2}$=$\frac{11}{2}$.
故答案为$\frac{11}{2}$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
17.一天,小明在家和学校之间行走,为了好奇,他测了一下在无风时的速度是50米/分,从家到学校用了15分钟,从原路返回用了18分钟20秒.设风的速度是x米/分,则所列方程为( )
| A. | 15(50+x)=18.2(50-x) | B. | 15(50-x)=18.2(50+x) | C. | 15(50+x)=$\frac{55}{3}$(50-x) | D. | 15(50-x)=$\frac{55}{3}$(50+x) |
13.-$\frac{2}{3}$的倒数是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{3}{2}$ |
14.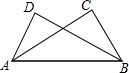 如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )
如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )
 如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )
如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )| A. | 60° | B. | 35° | C. | 85° | D. | 不能确定 |