题目内容
19.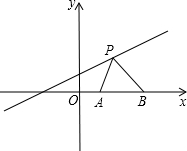 已知如图,点A(1,0),点B(2,0),点P是直线y=$\frac{1}{2}$x+1上的一个动点,PA2+PB2的最小值=$\frac{27}{5}$.
已知如图,点A(1,0),点B(2,0),点P是直线y=$\frac{1}{2}$x+1上的一个动点,PA2+PB2的最小值=$\frac{27}{5}$.
分析 设P(a,$\frac{1}{2}$a+1),根据两点间的距离公式得到PA2+PB2=(a-1)2+($\frac{1}{2}$a+1)2+(a-2)2+($\frac{1}{2}$a+1)2,化简得到PA2+PB2=$\frac{5}{2}$(a-$\frac{4}{5}$)2+$\frac{27}{5}$,根据二次函数的最值的求法即可得到结论.
解答 解:设P(a,$\frac{1}{2}$a+1),
∵A(1,0),点B(2,0),
∴PA2+PB2=(a-1)2+($\frac{1}{2}$a+1)2+(a-2)2+($\frac{1}{2}$a+1)2,
∴PA2+PB2=$\frac{5}{2}$a2-4a+7=$\frac{5}{2}$(a-$\frac{4}{5}$)2+$\frac{27}{5}$,
∴PA2+PB2的最小值=$\frac{27}{5}$,
故答案为:$\frac{27}{5}$.
点评 本题考查了最小值问题,两点间的距离公式,一次函数图象上的坐标特征,熟练掌握两点间的距离公式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列函数中,当x>0时,y随x增大而增大的是( )
| A. | y=-x | B. | y=$\frac{1}{x}$ | C. | y=3-2x | D. | y=x2 |
11.下列各式中,是最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{30}$ | C. | $\sqrt{\frac{1}{5}}$ | D. | $\frac{1}{{\sqrt{x}}}$ |