题目内容
19．化简$\frac{1}{3-2\sqrt{2}}$结果正确的是（ ）| A． | 3$+2\sqrt{2}$ | B． | 3$-\sqrt{2}$ | C． | 17$+12\sqrt{2}$ | D． | 17-12$\sqrt{2}$ |
分析 原式分子分母乘以有理化因式，计算即可得到结果．
解答 解：原式=$\frac{3+2\sqrt{2}}{（3-2\sqrt{2}）（3+2\sqrt{2}）}$
=3+2$\sqrt{2}$．
故选A．
点评 此题考查了分母有理化，找出原式的有理化因式是解本题的关键．
练习册系列答案
相关题目
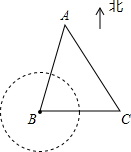南沙群岛自古以来就是中国的领土，但南沙群岛中只哟部分岛屿受中国的控制，赤瓜礁就是其中之一．以赤瓜礁为圆心，在周围12海里范围内均属于禁区，不允许他国船只进入．今有一中国海监船（记作A）正以14海里/小时的速度在位于赤瓜礁（记作B）北偏东15°的海域中巡逻，海监船上的值班人员发现在赤瓜礁的正东方向24海里有一艘外国渔船（记作C），其正以10海里/小时的速度沿正西方向驶向赤瓜礁，中方立即向外国渔船发出警告，此时外国渔船在中国海监船的南偏东30°的方向上，如图所示．
14．两条直线相交所成的四个角都相等时，这两条直线的位置关系是（ ）
| A． | 平行 | B． | 相交 | C． | 垂直 | D． | 不能确定 |
11．下列各式中，是最简二次根式的是（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{30}$ | C． | $\sqrt{\frac{1}{5}}$ | D． | $\frac{1}{{\sqrt{x}}}$ |
8．下列说法错误的是（ ）
| A． | 绝对值最小的数是0 | B． | 最小的自然数是1 | ||
| C． | 最大的负整数是-1 | D． | 绝对值小于2的整数是：1，0，-1 |