题目内容
19.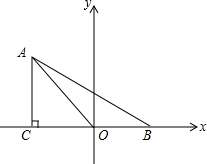 如图,在平面直角坐标系中,已知点A(xA,2)在第二象限,AC⊥x轴于点C,△AOC的面积为$\sqrt{3}$,点B的坐标为($\sqrt{3}$,0).
如图,在平面直角坐标系中,已知点A(xA,2)在第二象限,AC⊥x轴于点C,△AOC的面积为$\sqrt{3}$,点B的坐标为($\sqrt{3}$,0).(1)求AB的长及∠ABC的度数;
(2)以AB为一边作等边三角形ABP,求点P的坐标.
分析 (1)根据A(xA,2),AC⊥x轴于点C,得到AC=2,由△AOC的面积为$\sqrt{3}$,得到OC=$\sqrt{3}$,OB=$\sqrt{3}$,根据勾股定理得到AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=4;根据三角函数的定义得到结论;
(2)①当P在第一象限时,由于∠ABP=60°,∠ABC=30°,得到∠PBC=90°,推出PB⊥x轴,求得P($\sqrt{3}$,4),②当P在第三象限时,由∠ABC=30°,∠ABP=60°,得到∠CBP=30°,得到AP′⊥x轴,求得P′(-$\sqrt{3}$,-$\sqrt{3}$).
解答 解:(1)∵A(xA,2),AC⊥x轴于点C,
∴AC=2,
∵△AOC的面积为$\sqrt{3}$,
∴$\frac{1}{2}$AC•OC=$\sqrt{3}$,
∴OC=$\sqrt{3}$,
∵点B的坐标为($\sqrt{3}$,0),
∴OB=$\sqrt{3}$,
∴BC=2$\sqrt{3}$,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=4;
∵tan∠ABC=$\frac{AC}{BC}=\frac{\sqrt{3}}{3}$,
∴∠ABC=30°;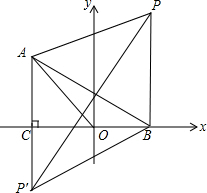 (2)如图,∵AB为一边作等边三角形ABP,
(2)如图,∵AB为一边作等边三角形ABP,
∴P在AB的垂直平分线上,
∴点P在第一、三象限,
①当P在第一象限时,
∵∠ABP=60°,∠ABC=30°,
∴∠PBC=90°,
∴PB⊥x轴,
∴P($\sqrt{3}$,4),
②当P在第三象限时,
∵∠ABC=30°,∠ABP=60°,
∴∠CBP=30°,
∵∠AP′B=60°,
∴AP′⊥x轴,
∴P′(-$\sqrt{3}$,-2).
点评 本题考查了等边三角形的性质,坐标与图形的性质,正确的作出图形是解题的关键.

 如图,PA、PB是⊙O的切线,AC是⊙O直径,∠c=55°,则∠APB等于( )
如图,PA、PB是⊙O的切线,AC是⊙O直径,∠c=55°,则∠APB等于( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
 如图,将矩形纸ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E,若CD=6,AD=18,则BE=10.
如图,将矩形纸ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E,若CD=6,AD=18,则BE=10.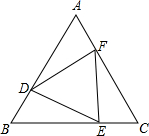 如图,D、E、F分别是等边△ABC各边上的点,且BD=CE=2,BE=CF.
如图,D、E、F分别是等边△ABC各边上的点,且BD=CE=2,BE=CF. 如图,在△AOB中,O是坐标原点,AB=0B,A(1,3),点C在直线y=-x+1上.
如图,在△AOB中,O是坐标原点,AB=0B,A(1,3),点C在直线y=-x+1上.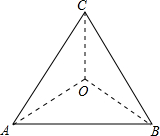 如图,边长为3的等边△ABC内一点O到三个顶点的距离都相等,则OA=$\sqrt{3}$.
如图,边长为3的等边△ABC内一点O到三个顶点的距离都相等,则OA=$\sqrt{3}$.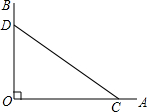 画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.
画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.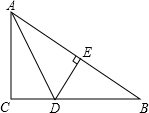 △ABC中,∠C=90°,AD为角平分线,BC=64,BD:DC=9:7,求D到AB的距离.
△ABC中,∠C=90°,AD为角平分线,BC=64,BD:DC=9:7,求D到AB的距离.