题目内容
17.如图,AB为⊙O的直径,CF切⊙O于点C,BF⊥CF于点F,点D在⊙O上,CD交AB于点E,∠BCE=∠BCF.(1)求证:弧AC=弧AD;
(2)点G在⊙O上,∠GCD=∠FCD,连接DO并延长交CG于点H,求证:CH=GH;
(3)在(2)的条件下,连接AG,AG=3,CF=2$\sqrt{13}$,求CG的长.
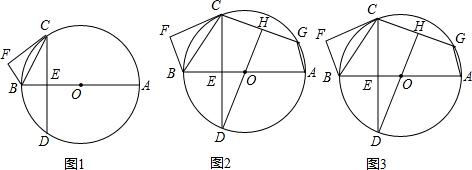
分析 (1)如图1,连接半径,根据切线的性质得出垂直,与已知BF⊥FC,得BF∥OC,所以∠BEC=∠BFC=90°,由垂径定理得:弧AC=弧AD;
(2)如图2,根据同圆半径相等得∠OCD=∠D,由切线的性质得∠FCD+∠OCD=90°,根据等量代换得:
∠DCG+∠D=90°,所以∠DHC=90°,由垂径定理得CH=HG;
(3)如图3中,延长GA到M,使得AD=AM,连接DM,延长CG到N,使得GN=GD,连接AN,作DJ⊥AM于J.首先证明△CAD≌△MAD,得AM=AC,DM=CD=DG,同理可得GN=DG,AN=AD=AC,再证明DM2-DA2=(DJ2+JM2)-(DJ2+AJ2)=(JM+AJ)(JM-AJ)=AM•AG,求出AD,同理可得AN2-AG2=GN•CG,延长即可解决问题.
解答 证明:(1)如图1,连接OC,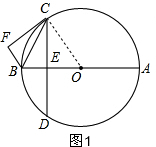
∵OC=OB,
∴∠OBC=∠OCB,
∵FC是⊙O的切线,
∴OC⊥FC,
∵BF⊥FC,
∴BF∥OC,∠BFC=90°,
∴∠OCB=∠FBC,
∴∠OBC=∠FBC,
∵∠BCE=∠BCF,
∴△FBC∽△EBC,
∴∠BEC=∠BFC=90°,
∴OB⊥DC,
∴弧AC=弧AD;
(2)如图2,连接OC.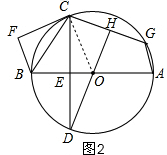
∵OC=OD,
∴∠OCD=∠D,
∵FC是⊙O的切线,
∴∠FCD+∠OCD=90°,
∵∠FCD=∠DCG,
∴∠DCG+∠D=90°,
∴∠DHC=90°,
∴DH⊥CG,
∵DH经过圆心O,
∴CH=HG.
(3)如图3中,延长GA到M,使得AD=AM,连接DM,延长CG到N,使得GN=GD,连接AN,作DJ⊥AM于J.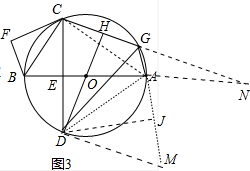
∵CE=CF=2$\sqrt{13}$,
∴CD=2$\sqrt{13}$,
∵DC=DG,AC=AD,
∵∠DAM=∠DCG=∠CAD,
∴△CAD≌△MAD,
∴AM=AC,DM=CD=DG,
同理可证GN=DG,AN=AD=AC,
∵DM2-DA2=(DJ2+JM2)-(DJ2+AJ2)=(JM+AJ)(JM-AJ)=AM•AG,
∴(4$\sqrt{13}$)2-AD2=AD•3,
j解得AD=13,
同理在等腰三角形△NAC中可得AN2-AG2=GN•CG,
∴169-9=4$\sqrt{13}$•CG,
∴CG=$\frac{40\sqrt{13}}{13}$.
点评 本题考查圆综合题、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加辅助线,构造全等三角形,记住一些基本图形、基本结论,属于中考压轴题.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案 如图,已知∠ABC=∠DCE=90°,AC⊥DE,则图中共有相似三角形的对数为( )
如图,已知∠ABC=∠DCE=90°,AC⊥DE,则图中共有相似三角形的对数为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
| A. | 6,8 | B. | 3,2 | C. | 2,3 | D. | 3,4 |
| A. | 3x+6=2x | B. | y-$\frac{x}{2}$=4 | C. | 2x=y2+1 | D. | xy=3 |
| A. | 5 | B. | 4 | C. | 6 | D. | 7 |
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
 如图,在平面直角坐标中,点A的坐标为(4,0),直线AB⊥x轴,直线y=-$\frac{1}{4}$x+3经过点B,与y轴交于点C.
如图,在平面直角坐标中,点A的坐标为(4,0),直线AB⊥x轴,直线y=-$\frac{1}{4}$x+3经过点B,与y轴交于点C.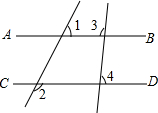 如图,已知直线AB、CD被直线l1,l2所截,若∠1+∠2=180°,∠3=98°,则∠4的度数为82°.
如图,已知直线AB、CD被直线l1,l2所截,若∠1+∠2=180°,∠3=98°,则∠4的度数为82°.