题目内容
19.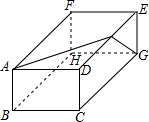 如图是一个长方体,AB=3,BC=5,AF=6.要在长方体上系一根绳子连接A、G,则绳子至少要多长?(接头处长度不计)
如图是一个长方体,AB=3,BC=5,AF=6.要在长方体上系一根绳子连接A、G,则绳子至少要多长?(接头处长度不计)
分析 分为三种情况展开,根据勾股定理求出线段AB的长度,再进行比较即可.
解答 解:如图1所示:AC=AD+DC=5+3=8,CG=6.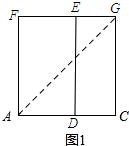
在Rt△ACG中,$AG=\sqrt{A{C}^{2}+C{G}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10;
如图2所示,BG=BC+CG=5+6=11,EG=3,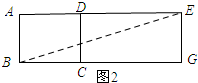
在Rt△BGE中,$BE=\sqrt{B{G}^{2}+E{G}^{2}}$=$\sqrt{1{1}^{2}+{3}^{2}}$=$\sqrt{130}$;
如图3所示:
GD=DE+EG=3+6=9,AD=5.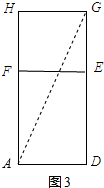
在Rt△ADG中,$AG=\sqrt{A{D}^{2}+G{D}^{2}}$=$\sqrt{{5}^{2}+{9}^{2}}$=$\sqrt{106}$.
∵100<106<130,
∴$\sqrt{100}<\sqrt{106}<\sqrt{130}$,即10$<\sqrt{106}<\sqrt{130}$.
∴绳子的长度至少为10.
点评 本题考查了平面展开-最短路线问题和勾股定理等知识点,关键是能画出展开图形并能求出符合条件的最短路线.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
15.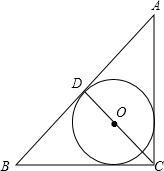 在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )
在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )
 在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )
在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )| A. | CD | B. | BC | C. | AC | D. | AB |
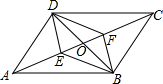 如图,在?ABCD,对角线AC、BD相交于点O、E、F是对角线AC上的两点.
如图,在?ABCD,对角线AC、BD相交于点O、E、F是对角线AC上的两点. 如图,在△ABC中,若D、E分别是AB、AC上的点,且DE∥BC,AD=1,BD=2,则DE:BC=1:3.
如图,在△ABC中,若D、E分别是AB、AC上的点,且DE∥BC,AD=1,BD=2,则DE:BC=1:3.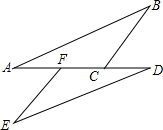 如图,在△ABC和△DEF中,AF=DC,∠A=∠D.当添加条件BC=EF时,可依据“SAS”证明△ABC≌△DEF;当添加条件∠ACB=∠DFE时,可依据”ASA”证明△ABC≌△DEF,当添加条件∠B=∠E时,可依据”AAS”证明△ABC≌△DEF.
如图,在△ABC和△DEF中,AF=DC,∠A=∠D.当添加条件BC=EF时,可依据“SAS”证明△ABC≌△DEF;当添加条件∠ACB=∠DFE时,可依据”ASA”证明△ABC≌△DEF,当添加条件∠B=∠E时,可依据”AAS”证明△ABC≌△DEF. 如图,已知线段AC,BD相交于点O,且OA=OC,OB=OD,E,F分别为DO,BO上两点,DE=BF,CE=9,求AF的长.
如图,已知线段AC,BD相交于点O,且OA=OC,OB=OD,E,F分别为DO,BO上两点,DE=BF,CE=9,求AF的长.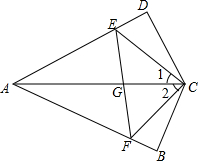 如图所示,∠1=∠2,CD⊥AD,CB⊥AB.CD=CB,AC、EF相交于点G.求证:AC垂直平分EF.
如图所示,∠1=∠2,CD⊥AD,CB⊥AB.CD=CB,AC、EF相交于点G.求证:AC垂直平分EF.