题目内容
9.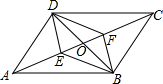 如图,在?ABCD,对角线AC、BD相交于点O、E、F是对角线AC上的两点.
如图,在?ABCD,对角线AC、BD相交于点O、E、F是对角线AC上的两点.(1)现有三个条件:①∠ADE=∠CBF;②∠ABE=∠CDF;③AE=CF都可确定四边形DEBF为平行四边形.
(2)请选择其中的一个等式作为条件,证明四边形DEBF为平行四边形.
分析 选择③,由四边形ABCD为平行四边形,得到对角线互相平分,再由AE=CF,得到OE=OF,利用对角线互相平分的四边形为平行四边形即可得证.
解答 解:选择③AE=CF,理由为:
证明:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF,
∴四边形DEBF为平行四边形.
点评 此题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 已知:如图,点C为AB中点,CD=BE,CD∥BE.
已知:如图,点C为AB中点,CD=BE,CD∥BE. 已知:如图,点A、B、C、D在同一条直线上,AC=DB,∠ABE=∠DCF,BE=CF,求证:AE∥DF.
已知:如图,点A、B、C、D在同一条直线上,AC=DB,∠ABE=∠DCF,BE=CF,求证:AE∥DF.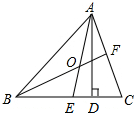 如图,在△ABC中,AD是高,AE和BF是角平分线,它们相交于点O,∠ABC=60°,∠C=70°,求∠CAD和∠AOF的度数.
如图,在△ABC中,AD是高,AE和BF是角平分线,它们相交于点O,∠ABC=60°,∠C=70°,求∠CAD和∠AOF的度数.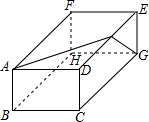 如图是一个长方体,AB=3,BC=5,AF=6.要在长方体上系一根绳子连接A、G,则绳子至少要多长?(接头处长度不计)
如图是一个长方体,AB=3,BC=5,AF=6.要在长方体上系一根绳子连接A、G,则绳子至少要多长?(接头处长度不计)