题目内容
1. 如图,正方形的边长为2,则AC=2$\sqrt{2}$,面积是4.
如图,正方形的边长为2,则AC=2$\sqrt{2}$,面积是4.
分析 由勾股定理求出AC,利用正方形的面积计算公式直接计算得出答案即可.
解答 解:∵四边形ABCD是正方形,
∴∠B=90°,AB=BC=2,
∴AC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,正方形的面积为2×2=4.
故答案为:$2\sqrt{2}$,4.
点评 此题考查正方形的性质、勾股定理,掌握正方形的性质是解决问题的关键.

练习册系列答案
相关题目
13.已知,点A(-2,y1)、B(1,y2)在直线y=-2x+3上,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 无法确定 |
 如图,已知:AB⊥BC于B,EF⊥AC于G,DF⊥BC 于D,BC=DF.猜想线段AC与EF的数量关系,并证明你的结论.
如图,已知:AB⊥BC于B,EF⊥AC于G,DF⊥BC 于D,BC=DF.猜想线段AC与EF的数量关系,并证明你的结论.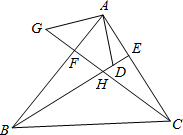 如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD.AG.
如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD.AG.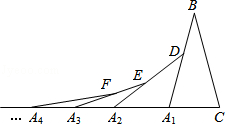 如图,在第一个△A1BC中,∠B=30°,A1B=CB,在边A1B上任取一D,延长CA2到A2,使A1A2=A1D,得到第2个△A1A2D,在边A2B上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第三个△A2A3E,…按此做法继续下去,第n个等腰三角形的底角的度数是$\frac{75}{{2}^{n-1}}$度.
如图,在第一个△A1BC中,∠B=30°,A1B=CB,在边A1B上任取一D,延长CA2到A2,使A1A2=A1D,得到第2个△A1A2D,在边A2B上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第三个△A2A3E,…按此做法继续下去,第n个等腰三角形的底角的度数是$\frac{75}{{2}^{n-1}}$度.