题目内容
9. 如图,已知:AB⊥BC于B,EF⊥AC于G,DF⊥BC 于D,BC=DF.猜想线段AC与EF的数量关系,并证明你的结论.
如图,已知:AB⊥BC于B,EF⊥AC于G,DF⊥BC 于D,BC=DF.猜想线段AC与EF的数量关系,并证明你的结论.
分析 结论:AC=EF.只要证明△ABC≌△EDF,即可解决问题.
解答 解:结论:AC=EF.理由如下,
∵AB⊥BC于B,EF⊥AC于G,DF⊥BC于D,
∴∠ABC=∠EDF=∠CGE=90°,
∴∠C+∠CEF=90°,
∠F+∠CEF=90°,
∴∠C=∠F,
在△ABC与△EDF中
$\left\{\begin{array}{l}{∠ABC=∠EDF}\\{BC=DF}\\{∠C=∠F}\end{array}\right.$,
∴△ABC≌△EDF,
∴AC=EF.
点评 本题考查全等三角形的判定和性质,同角的余角相等等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
1.下列命题中,属于真命题的是( )
| A. | 同位角相等 | B. | 任意三角形的外角一定大于内角 | ||
| C. | 多边形的内角和等于180° | D. | 同角或等角的余角相等 |
18.观察下列钢管横截面图,则第13个图中钢管的个数是( )


| A. | 271 | B. | 269 | C. | 273 | D. | 267 |
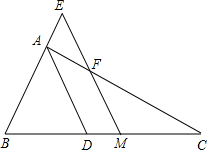 如图,△ABC中∠A的平分线为AD,M为BC的中点,过点M作ME∥AD交BA的延长线于E,交AC于F.
如图,△ABC中∠A的平分线为AD,M为BC的中点,过点M作ME∥AD交BA的延长线于E,交AC于F. 如图,正方形的边长为2,则AC=2$\sqrt{2}$,面积是4.
如图,正方形的边长为2,则AC=2$\sqrt{2}$,面积是4.