Question

11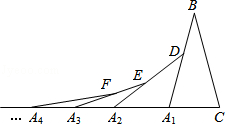．如图，在第一个△A₁BC中，∠B=30°，A₁B=CB，在边A₁B上任取一D，延长CA₂到A₂，使A₁A₂=A₁D，得到第2个△A₁A₂D，在边A₂B上任取一点E，延长A₁A₂到A₃，使A₂A₃=A₂E，得到第三个△A₂A₃E，…按此做法继续下去，第n个等腰三角形的底角的度数是$\frac{75}{{2}^{n-1}}$度．

Answer 1

分析 先根据等腰三角形的性质求出∠BA₁A的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠CA₂A₁，∠DA₃A₂及∠EA₄A₃的度数，找出规律即可得出第n个等腰三角形的底角的度数．

解答 解：∵在△ABA₁中，∠B=30°，AB=A₁B，
∴∠BA₁A=$\frac{180°-∠B}{2}$=75°，
∵A₁A₂=A₁D，∠BA₁C是△A₁A₂D的外角，
∴∠DA₂A₁=$\frac{1}{2}$∠BA₁C=$\frac{1}{2}$×75°=37.5°；
同理可得，
∠EA₃A₂=$\frac{75°}{4}$，∠FA₄A₃=$\frac{75°}{8}$，
∴第n个等腰三角形的底角的度数=$\frac{75°}{{2}^{n-1}}$．
故答案为$\frac{75}{{2}^{n-1}}$．

点评 本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠DA₂A₁，∠EA₃A₂及∠FA₄A₃的度数，进而找出规律是解答此题的关键．