Question

13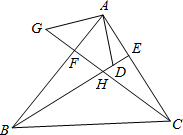．如图，在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD．AG．
（1）求证：AD=AG；
（2）AD与AG的位置关系如何．

Answer 1

分析 （1）先由条件可以得出∠ABE=∠ACF，就可以得出△ABD≌△GCA，就有AD=GA，∠BAD=∠G；
（2）结论：AG⊥AD．由（1）可以得出∠GAD=90°，进而得出AG⊥AD．

解答 解：（1）∵BE、CF分别是AC、AB两边上的高，
∴∠AFC=∠BFC=∠BEC=∠BEA=90°
∴∠BAC+∠ACF=90°，∠BAC+∠ABE=90°，∠G+∠GAF=90°，
∴∠ABE=∠ACF．
在△ABD和△GCA中，
$\left\{\begin{array}{l}{BD=AC}\\{∠ABE=∠ACF}\\{AB=CG}\end{array}\right.$，
∴△ABD≌△GCA（SAS），
∴AD=GA，

（2）结论：AG⊥AD．
理由：∵△ABD≌△GCA（SAS），
∴∠BAD=∠G，
∴∠BAD+∠GAF=90°，
∴AG⊥AD．

点评 本题考查了全等三角形的判定及性质的运用、直角三角形的性质等知识，解题的关键是熟练掌握全等三角形的判定和性质，学会利用等量代换证明垂直，属于中考常考题型．