题目内容
2.$\sqrt{3x+2y+6-m}+\sqrt{2x+3y-m}+\sqrt{x+y-2}=0$,则m的平方根为±$\frac{\sqrt{30}}{2}$.分析 先根据非负数的性质列出关于x、y、m的方程组,求出m的值,再由平方根的定义即可得出结论.
解答 解:∵$\sqrt{3x+2y+6-m}$+$\sqrt{2x+3y-m}$+$\sqrt{x+y-2}$=0,
∴$\left\{\begin{array}{l}3x+2y+5-m=0\\ 2x+3y-m=0\\ x+y-2=0\end{array}\right.$,解得m=$\frac{15}{2}$.
∴±$\sqrt{m}$=±$\sqrt{\frac{15}{2}}$=±$\frac{\sqrt{30}}{2}$.
故答案为:±$\frac{\sqrt{30}}{2}$.
点评 本题考查的是非负数的性质,熟知算术平方根具有非负性是解答此题的关键.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | 两个负数,绝对值大的大 | |
| B. | 在数轴上表示两个负数,离原点远的那个数小 | |
| C. | 两个数比较大小,绝对值大的反而小 | |
| D. | 在数轴上,两个负数中大的离原点远 |
1.已知a>1,点A(a-1,y1),B(a,y2),C(a+1,y3)都在二次函数y=-$\frac{1}{2}$x2的图象上,则( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
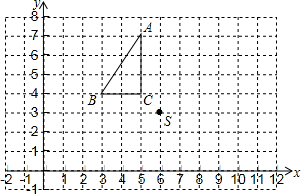 △ABC和点S在平面直角坐标系中的位置如图所示.
△ABC和点S在平面直角坐标系中的位置如图所示.