题目内容
9．下列命题中，真命题是（ ）| A． | 正数有两个立方根 | |
| B． | 0没有平方根 | |
| C． | $\sqrt{2}$是无理数 | |
| D． | 两边及其中一边的对角分别相等的两个三角形是全等三角形 |
分析 根据立方根的定义对A进行判断；根据0的平方根为0对B进行判断；根据无理数的定义对C进行判断；根据全等三角形的判定方法对D进行判断．
解答 解：A、任何实数的立方根只有一个，所以A选项错误；
B、0的平方根为0，所以B选项错误；
C、$\sqrt{2}$为无理数，所以C选项正确；
D、两边和它们的夹角分别相等的两个三角形是全等三角形，所以D选项错误．
故选C．
点评 本题考查了命题与定理：命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．
练习册系列答案
轻松暑假总复习系列答案
相关题目
如图，AM是△ABC的中线，∠C=90°，MN⊥AB于N，求证：AN2-BN2=AC2．
14．
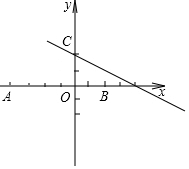如图，已知点A，B的坐标分别为（-4，0）和（2，0），在直线l：y=-$\frac{1}{2}$x+2上取一点C，若△ABC是直角三角形，则满足条件的点C有（ ）
如图，已知点A，B的坐标分别为（-4，0）和（2，0），在直线l：y=-$\frac{1}{2}$x+2上取一点C，若△ABC是直角三角形，则满足条件的点C有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
1．
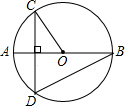如图，线段AB是⊙O的直径，弦CD⊥AB，∠OCD=40°，则∠ABD的度数是（ ）
如图，线段AB是⊙O的直径，弦CD⊥AB，∠OCD=40°，则∠ABD的度数是（ ）| A． | 20° | B． | 25° | C． | 30° | D． | 40° |
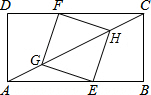如图，矩形ABCD中，AB=8，BC=4，点E在AB上，点F在CD上，点G、H在对角线AC上，若四边形EGFH是正方形，则AG的长是$\sqrt{5}$．