题目内容
1．
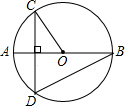如图，线段AB是⊙O的直径，弦CD⊥AB，∠OCD=40°，则∠ABD的度数是（ ）| A． | 20° | B． | 25° | C． | 30° | D． | 40° |
分析 先根据垂径定理得到$\widehat{AC}=\widehat{AD}$，再根据圆周角定理得∠AOC=2∠ABD=50°，计算∠ABD的度数．
解答 
解：∵CD⊥AB，
∴$\widehat{AC}$=$\widehat{AD}$，∠CEO=90°
∵∠OCD=40°
∴∠AOC=90°-40°=50°
∵∠AOC=2∠ABD，
∴∠ABD=25°．
故选B．
点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了垂径定理．
练习册系列答案
相关题目
11．
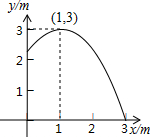如图，池中心竖直水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管的长为（ ）
如图，池中心竖直水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管的长为（ ）| A． | 2.1m | B． | 2.2m | C． | 2.3m | D． | 2.25m |
9．下列命题中，真命题是（ ）
| A． | 正数有两个立方根 | |
| B． | 0没有平方根 | |
| C． | $\sqrt{2}$是无理数 | |
| D． | 两边及其中一边的对角分别相等的两个三角形是全等三角形 |
16．下列各式计算正确的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B． | a2+a3=a5 | C． | $\frac{1}{y}$-$\frac{1}{x}$=x-y | D． | （-a3b）2=a6b2 |
如图，已知一次函数y=kx+b，则当x＜2.5时，kx+b＜0．