题目内容
12.计算:$\sqrt{96}$=4$\sqrt{6}$,$-\sqrt{2\frac{1}{4}}$=-$\frac{3}{2}$,$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,$\sqrt{18{x}^{2}{y}^{3}}$(x>0,y>0)=3xy$\sqrt{2y}$.分析 直接利用二次根式的性质化简求出答案.
解答 解:$\sqrt{96}$=4$\sqrt{6}$,
$-\sqrt{2\frac{1}{4}}$=-$\sqrt{\frac{9}{4}}$=-$\frac{3}{2}$,
$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,
$\sqrt{18{x}^{2}{y}^{3}}$(x>0,y>0)=3xy$\sqrt{2y}$.
故答案为:4$\sqrt{6}$,-$\frac{3}{2}$,$\frac{\sqrt{6}}{3}$,3xy$\sqrt{2y}$.
点评 此题主要考查了二次根式的性质,正确掌握二次根式的性质是解题关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
20. 若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )
若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )
 若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )
若有理数在数轴上的位置如图所示,则化简:|a+c|-|a-b|-|c-b|的结果为( )| A. | 0 | B. | -2a | C. | -2b | D. | -2c |
4.在数轴上,原点左边的点表示的数是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
1.下列计算中,不正确的是( )
| A. | 3$\sqrt{2}$×2$\sqrt{5}$=6$\sqrt{10}$ | B. | 3$\sqrt{6}$÷3$\sqrt{7}$=$\frac{6}{7}$ | C. | $\sqrt{2}$-5$\sqrt{2}$=-4$\sqrt{2}$ | D. | (3$\sqrt{2}$+2$\sqrt{3}$ )( 3$\sqrt{2}$-2$\sqrt{3}$)=6 |
2.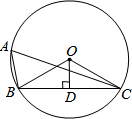 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
 一个几何体由几个大小相同的小正方体搭成,其左视图和俯视图如图所示,则搭成这个几何体的小正方体的个数是( )
一个几何体由几个大小相同的小正方体搭成,其左视图和俯视图如图所示,则搭成这个几何体的小正方体的个数是( )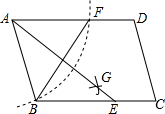 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )