题目内容
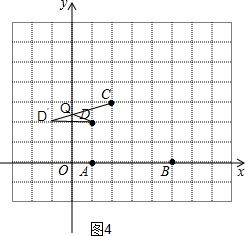
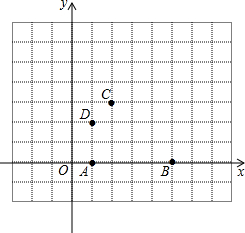 如图,在同一平面直角坐标系中有4个点:A(1,0),B(5,0),C(2,3),D(1,2).
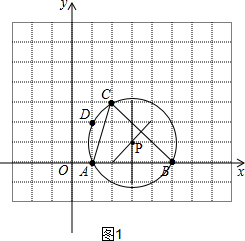
如图,在同一平面直角坐标系中有4个点:A(1,0),B(5,0),C(2,3),D(1,2).(1)画出△ABC的外切圆⊙P,并指出点D与⊙P的位置关系;
(2)判断直线OD与⊙P的位置关系,说明理由;
(3)计算sin∠ACB的值;
(4)若在y轴上有一动点Q,当|QC-QD|最小时,点Q的坐标为
考点:圆的综合题
专题:
分析:(1)先确定圆心点P,画圆即可.
(2)直线OD与⊙P相切.连接OD,DP,OP,求出OD,DP,OP的值,利用勾股定理的逆定理可得△ODP是直角三角形,即可得出直线OD与⊙P相切.
(3)利用∠ACB=∠ADB,求sin∠ACB即可,
(4)①连接CD作CD的中垂线交y轴于点Q,此时|QC-QD|=0最小;②作点D关于y轴的对称点D′,连接D′C交y轴于点Q,此时QC+QD最小,分别求解得出Q的坐标即可.
(2)直线OD与⊙P相切.连接OD,DP,OP,求出OD,DP,OP的值,利用勾股定理的逆定理可得△ODP是直角三角形,即可得出直线OD与⊙P相切.
(3)利用∠ACB=∠ADB,求sin∠ACB即可,
(4)①连接CD作CD的中垂线交y轴于点Q,此时|QC-QD|=0最小;②作点D关于y轴的对称点D′,连接D′C交y轴于点Q,此时QC+QD最小,分别求解得出Q的坐标即可.
解答:解:(1)如图1,点D在⊙P上,
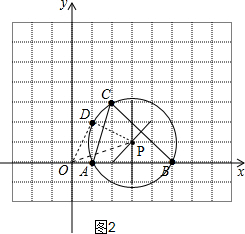
(2)直线OD与⊙P相切.
理由如下:
如图2,连接OD,DP,OP,
OP=
,OD=
,DP=
,
∵(
)2+(
)2=(
)2,
∴OD2+DP2=OP2,
∴△ODP是直角三角形,
∴∠ODP=90°,
∴直线OD与⊙P相切.
(3)∵∠ACB=∠ADB,
∴sin∠ACB=sin∠ADB=
=
=
.
(4)①连接CD作CD的中垂线交y轴于点Q,此时|QC-QD|=0最小,点Q的坐标为(4,0)
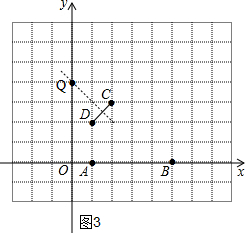
②作点D关于y轴的对称点D′,连接D′C交y轴于点Q,此时QC+QD最小,
∵点D(1,2),
∴D′(-1,2),
设CD′所在的直线的解析式为y=kx+b,把D′(-1,2),C(2,3),代入得
,
解得
,
∴CD′所在的直线的解析式为y=
x+
,
当x=0时,y=
,
∴Q(
,0).
故答案为:(4,0),(
,0).

(2)直线OD与⊙P相切.
理由如下:
如图2,连接OD,DP,OP,

OP=
| 10 |
| 5 |
| 5 |
∵(
| 5 |
| 5 |
| 10 |
∴OD2+DP2=OP2,
∴△ODP是直角三角形,
∴∠ODP=90°,
∴直线OD与⊙P相切.
(3)∵∠ACB=∠ADB,
∴sin∠ACB=sin∠ADB=
| AB |
| BD |
| 4 | ||
|
2
| ||
| 5 |
(4)①连接CD作CD的中垂线交y轴于点Q,此时|QC-QD|=0最小,点Q的坐标为(4,0)

②作点D关于y轴的对称点D′,连接D′C交y轴于点Q,此时QC+QD最小,

∵点D(1,2),
∴D′(-1,2),
设CD′所在的直线的解析式为y=kx+b,把D′(-1,2),C(2,3),代入得
|
解得
|
∴CD′所在的直线的解析式为y=
| 1 |
| 3 |
| 7 |
| 3 |
当x=0时,y=
| 7 |
| 3 |
∴Q(
| 7 |
| 3 |
故答案为:(4,0),(
| 7 |
| 3 |
点评:本题主要考查了圆的综合题,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
已知x2-xy=3,3xy+y2=5,则2x2+xy+y2的值是( )
| A、8 | B、2 | C、11 | D、13 |
 如图,点C在线段AB上,且AC=6,BC=14,点M,N分别是AC,BC的中点,则线段MN的长度为( )
如图,点C在线段AB上,且AC=6,BC=14,点M,N分别是AC,BC的中点,则线段MN的长度为( )| A、10 | B、20 | C、7 | D、8 |
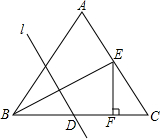 如图,在△ABC中,AB=AC,BC=8,E是AC的中点,且点B与点E关于直线l对称,EF⊥BC于F,若CF=2,EF=3,直线l与BC交于点D,则BD长为
如图,在△ABC中,AB=AC,BC=8,E是AC的中点,且点B与点E关于直线l对称,EF⊥BC于F,若CF=2,EF=3,直线l与BC交于点D,则BD长为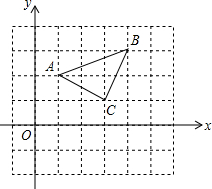 如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).把△A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,试写出△A1B1C1三个顶点的坐标.
如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).把△A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,试写出△A1B1C1三个顶点的坐标.