题目内容
已知x2-xy=3，3xy+y2=5，则2x2+xy+y2的值是（ ）
| A、8 | B、2 | C、11 | D、13 |
考点：整式的加减
专题：计算题
分析：第一个等式两边乘以2，与第二个等式相加即可求出原式的值．
解答：解：x2-xy=3①，3xy+y2=5②，
①×2+②得：2x2-2xy+3xy+y2=2x2+xy+y2=11．
故选C．
①×2+②得：2x2-2xy+3xy+y2=2x2+xy+y2=11．
故选C．
点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
如果单项式-2xa+1y3和3x2yb是同类项，那么a，b的值分别是（ ）
| A、a=1，b=3 |
| B、a=1，b=2 |
| C、a=2，b=3 |
| D、a=2，b=2 |
a，b互为相反数，则下列说法正确的是（ ）
| A、a-b=0 | ||
| B、ab＜0 | ||
| C、a+b=0 | ||
D、
|
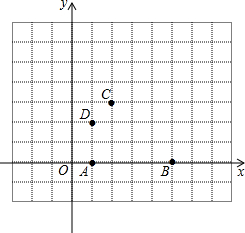如图，在同一平面直角坐标系中有4个点：A（1，0），B（5，0），C（2，3），D（1，2）．