题目内容
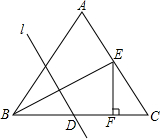 如图,在△ABC中,AB=AC,BC=8,E是AC的中点,且点B与点E关于直线l对称,EF⊥BC于F,若CF=2,EF=3,直线l与BC交于点D,则BD长为
如图,在△ABC中,AB=AC,BC=8,E是AC的中点,且点B与点E关于直线l对称,EF⊥BC于F,若CF=2,EF=3,直线l与BC交于点D,则BD长为考点:轴对称的性质
专题:
分析:连接DE,利用轴对称得出BD=DE,利用BC=8,CF=2,可得DF=6-BD,利用勾股定理得出(6-BD)2+32=BD2,即可得出BD的值.
解答:解:如图,连接DE,

∵点B与点E关于直线l对称,
∴BD=DE,
∵BC=8,CF=2,
∴DF=8-2-BD=6-BD,
∵EF⊥BC于F,EF=3,
∴DF2+EF2=DE2,即(6-BD)2+32=BD2,解得BD=
.
故答案为:
.

∵点B与点E关于直线l对称,
∴BD=DE,
∵BC=8,CF=2,
∴DF=8-2-BD=6-BD,
∵EF⊥BC于F,EF=3,
∴DF2+EF2=DE2,即(6-BD)2+32=BD2,解得BD=
| 15 |
| 4 |
故答案为:
| 15 |
| 4 |
点评:本题主要考查了轴对称的性质,解题的关键是正确作出辅助线,得出BD=DE.

练习册系列答案
相关题目
a,b互为相反数,则下列说法正确的是( )
| A、a-b=0 | ||
| B、ab<0 | ||
| C、a+b=0 | ||
D、
|
下列结论中正确的是( )
①由两条射线组成的图形叫角;②连接两点的线段叫两点之间的距离;③射线AB与射线BA是同一条直线;④∠AOB与∠BOA是同一角;⑤若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为补角;⑥两点之间线段最短.
①由两条射线组成的图形叫角;②连接两点的线段叫两点之间的距离;③射线AB与射线BA是同一条直线;④∠AOB与∠BOA是同一角;⑤若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为补角;⑥两点之间线段最短.
| A、④⑤ | B、④⑥ |
| C、①②⑥ | D、③④⑥ |
已知α是一个锐角的度数,β是一个钝角的度数,计算
(α+β)的结果可能是( )
| 1 |
| 6 |
| A、28° | B、48° |
| C、60° | D、88° |
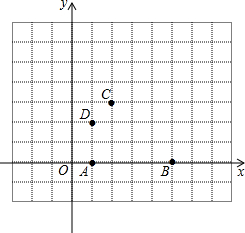 如图,在同一平面直角坐标系中有4个点:A(1,0),B(5,0),C(2,3),D(1,2).
如图,在同一平面直角坐标系中有4个点:A(1,0),B(5,0),C(2,3),D(1,2).